题目内容
6．
如图，在⊙O中，$\widehat{AB}$=$\widehat{AC}$，∠BAC=50°，则∠AEC的度数为（ ）| A． | 65° | B． | 75° | C． | 50° | D． | 55° |
分析 由在⊙O中，$\widehat{AB}$=$\widehat{AC}$，根据弧与弦的关系，可得AB=AC，然后由等腰三角形的性质，求得∠B的度数，又由圆周角定理，即可求得答案．
解答 解：∵在⊙O中，$\widehat{AB}$=$\widehat{AC}$，
∴AB=AC，
∵∠BAC=50°，
∴∠B=∠ACB=65°，
∴∠AEC=∠B=65°．
故选A．
点评 此题考查了圆周角定理以及弧与弦的关系．注意在同圆或等圆中，同弧或等弧所对的圆周角相等．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
14．
，若x=4，则y的值为（ ）
，若x=4，则y的值为（ ）| A． | 4 | B． | 10 | C． | 24 | D． | -4 |
1．
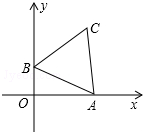如图，边长为2的等边△ABC的顶点A，B分别在x轴正半轴和y轴正半轴上运动，则动点C到原点O的距离的最大值是（ ）
如图，边长为2的等边△ABC的顶点A，B分别在x轴正半轴和y轴正半轴上运动，则动点C到原点O的距离的最大值是（ ）| A． | $\sqrt{3}-1$ | B． | $\sqrt{3}+1$ | C． | $\sqrt{6}-1$ | D． | $\sqrt{6}+1$ |
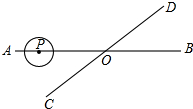如图，直线AB，CD相交于点O，∠AOC=30°，半径为1cm的圆P的圆心在直线AB上，且与点O的距离为10cm，如果⊙P以2cm∕s的速度，沿由A向B的方向移动，那么4或6秒钟后⊙P与直线CD相切．
如图，在△ABC中，∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的边于G，F，E点．
15．如果|-a|=a，则下列a的取值不能使这个式子成立的是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | a取任何负数 |
