题目内容
如图，某校计划在边长为a米的正方形场地上，修建两条宽为x（x＜a）米的通道，其余部分进行绿化．（1）请用两种方式计算通道的面积；
（2）判断a2+x2和2ax的数量关系，并利用图形说明理由．
考点：列代数式
专题：
分析：（1）可以直接计算两条通道的面积的和，也可以用正方形的面积减去草皮的面积；
（2）观察图形，即可得到a2+x2和2ax的数量关系．
（2）观察图形，即可得到a2+x2和2ax的数量关系．
解答：解：（1）①∵根据图形知：每条通道的长为a米，宽为x米，
∴每条通道的面积为ax，共为2ax米，重合部分的面积为x2，
∴甬道的面积为2×ax-x2=x（2a-x）（米2）；
②正方形的面积为a2米2，草皮的面积为（a-x）2米2，故甬道的面积为：a2-（a-x）2=x（2a-x）米2；
（2）观察图形，即可得到a2+x2＞2ax（x＜a）．
∴每条通道的面积为ax，共为2ax米，重合部分的面积为x2，
∴甬道的面积为2×ax-x2=x（2a-x）（米2）；
②正方形的面积为a2米2，草皮的面积为（a-x）2米2，故甬道的面积为：a2-（a-x）2=x（2a-x）米2；
（2）观察图形，即可得到a2+x2＞2ax（x＜a）．
点评：本题考查了因式分解的应用及列代数式的知识，解题的关键是分别表示出有关图形的面积并正确的利用因式分解．
练习册系列答案
相关题目
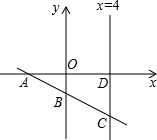如图，在直角坐标系内，一次函数y=kx+b（kb＞0，b＜0）的图象分别与x轴、y轴和直线x=4相交于A、B、C三点，直线x=4与x轴交于点D，四边形OBCD（O是坐标原点）的面积是10．若点A的横坐标是-
如图．在平面直角坐标系中．点A的坐标是（4，0），点P在第一象限，且在直线y=-x+6上，设点P的横坐标为a．△PAO的面积为S．