题目内容
如图甲,射线BC∥AD,一动点P从点A出发,沿如图的圆弧形曲线途径B、C两点向终点D运动,在运动过程中,我们研究所形成的三个角:∠APB、∠CBP、∠DAP的关系.

(1)如图甲,点P从点C向点D运动的过程中,求证:∠APB=∠CBP+∠DAP;
(2)如图乙,点P从点B向点C运动过程中,∠APB、∠CBP、∠DAP的三个角之间有怎样的关系(只写结论).

(1)如图甲,点P从点C向点D运动的过程中,求证:∠APB=∠CBP+∠DAP;
(2)如图乙,点P从点B向点C运动过程中,∠APB、∠CBP、∠DAP的三个角之间有怎样的关系(只写结论).
考点:平行线的性质
专题:
分析:(1)过点P作PQ∥BC,根据平行公理可得PQ∥AD,再根据两直线平行,内错角相等可得∠BPQ=∠CBP,∠APQ=∠DAP,然后根据∠APB=∠BPQ+∠APQ求解即可;
(2)过点P作PQ∥BC,根据平行公理可得PQ∥AD,根据两直线平行,同旁内角互补可得表示出∠QPB和∠QPA,再根据∠APB=∠QPB-∠QPA计算即可得解.
(2)过点P作PQ∥BC,根据平行公理可得PQ∥AD,根据两直线平行,同旁内角互补可得表示出∠QPB和∠QPA,再根据∠APB=∠QPB-∠QPA计算即可得解.
解答: (1)证明:如图,过点P作PQ∥BC,
(1)证明:如图,过点P作PQ∥BC,
∵BC∥AD,
∴PQ∥AD,
∴∠BPQ=∠CBP,∠APQ=∠DAP,
∵∠APB=∠BPQ+∠APQ,
∴∠APB=∠CBP+∠DAP;
(2)解:过点P作PQ∥BC,
∵BC∥AD,
∴PQ∥AD,
∴∠QPB=180°-∠CBP,∠QPA=180°-∠DAP,
∵∠APB=∠QPB-∠QPA,
∴∠APB=(180°-∠CBP)-(180°-∠DAP)=∠DAP-∠CBP,
即∠APB=∠DAP-∠CBP.
 (1)证明:如图,过点P作PQ∥BC,
(1)证明:如图,过点P作PQ∥BC,∵BC∥AD,
∴PQ∥AD,
∴∠BPQ=∠CBP,∠APQ=∠DAP,
∵∠APB=∠BPQ+∠APQ,
∴∠APB=∠CBP+∠DAP;
(2)解:过点P作PQ∥BC,
∵BC∥AD,
∴PQ∥AD,
∴∠QPB=180°-∠CBP,∠QPA=180°-∠DAP,
∵∠APB=∠QPB-∠QPA,
∴∠APB=(180°-∠CBP)-(180°-∠DAP)=∠DAP-∠CBP,
即∠APB=∠DAP-∠CBP.
点评:本题考查了平行线的性质,此类题目,过拐点作平行线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的最多个数是( )
如图,分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图,则组成这个几何体的小正方体的最多个数是( )| A、9个 | B、8个 | C、7个 | D、6 |
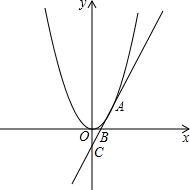 已知直线y1=2x-1分别交x轴、y轴于B、C,抛物线y2=mx2过直线y1=2x-1上点A(1,n).
已知直线y1=2x-1分别交x轴、y轴于B、C,抛物线y2=mx2过直线y1=2x-1上点A(1,n).
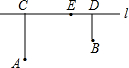 如图,在铁路L的同侧有A、B两村庄,已知A庄到L的距离AC=15km,B庄到L的距离BO=l0km,CD=25km.现要在铁路L上建一个土特产收购站E,使得A、B两村庄到E站的距离相等,
如图,在铁路L的同侧有A、B两村庄,已知A庄到L的距离AC=15km,B庄到L的距离BO=l0km,CD=25km.现要在铁路L上建一个土特产收购站E,使得A、B两村庄到E站的距离相等, 如图,已知O为直线AC上一点,OB为射线,OM、ON分别是∠AOB、∠COB的平分线,求∠MON的度数.
如图,已知O为直线AC上一点,OB为射线,OM、ON分别是∠AOB、∠COB的平分线,求∠MON的度数. 作图与证明 按下列要求尺规作图(保留作图痕迹):
作图与证明 按下列要求尺规作图(保留作图痕迹): 如图,直线a∥b,一个含有30°角的直角三角板放置在如图所示的位置,若∠1=24°,则∠2=
如图,直线a∥b,一个含有30°角的直角三角板放置在如图所示的位置,若∠1=24°,则∠2=