题目内容
10.因式分解:(1)3x-12x3
(2)-2a3+12a2-18a
(3)9a2(x-y)+4b2(y-x)
(4)(x+y)2+2(x+y)+1
(5)a2-2ab+b2-1.
分析 (1)根据提公因式法,可得平方差公式,根据平方差公式,可得答案;
(2)根据提公因式法,可得完全平方公式,根据完全平方公式,可得答案;
(3)根据提公因式法,可得平方差公式,根据平方差公式,可得答案;
(4)根据完全平方公式,可得答案;
(5)根据根据分组法,可得完全平方公式,根据完全平方公式,可得平方差公式,根据平方差公式,可得答案.
解答 解:(1)原式=3x(1-4x2)=3x(1+2x)(1-2x);
(2)原式=-2a(a2-6a+9)=-2a(a-3)2;
(3)原式=9a2(x-y)-4b2(x-y)=(x-y)(9a2-4b2)=(x-y)(3a+2b)(3a-2b);
(4)原式=[(x+y)+1]2=(x+y+1)2;
(5)原式=(a2-2ab+b2)-1=(a-b)2-1=(a-b+1)(a-b-1).
点评 本题考查了因式分解,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
19.已知抛物线y=ax2+bx-2与x轴没有交点,过A(-$\frac{13}{7}$、y1)、B(-3,y2)、C(1,y2)、D($\sqrt{3}$,y3)四点,则y1、y2、y3的大小关系是( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y1>y3>y2 | D. | y3>y2>y1 |
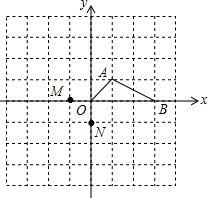 如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.
如图,在平面直角坐标系中有A(1,1)、B(3,0)两点.