题目内容
12.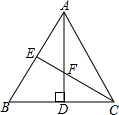 如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.
如图,在等边三角形ABC中,AD、CE分别是BC、AB边上的高,且AD、CE相交于点F.(1)求∠AFE的度数;
(2)若点D、E分别在BC、AB上运动,要想使结论(1)成立,请你猜想一下BD与AE应满足什么数量关系?并给出证明.
分析 (1)根据等边三角形三线合一的性质和高的性质即可证得∠AFE=60°;
(2)由∠AFE=60°=∠BAC,根据三角形外角的性质得出∠BAD=∠ACE,然后根据AAS证得△ABD≌△CAE即可证得BD=AE.
解答 解:(1)∵在等边三角形ABC中,AD、CE分别是BC、AB边上的高,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=30°,∠AEC=90°,
∴∠AFE=90°-∠EAF=90°-30°=60°;
(2)BD=AE,
∵△ABC是等边△ABC,
∴∠B=∠BAC=60°,AB=BC,
∵∠AFE=60°,
∠AFE=∠BAC,
∵∠BEC=∠ACE+∠BAC=∠BAD+∠FAE,
∴∠BAD=∠ACE,
在△ABD和△CAE中
$\left\{\begin{array}{l}{∠BAD=∠ACE}\\{∠ABD=∠EAC}\\{AB=AC}\end{array}\right.$
∴△ABD≌△CAE(AAS),
∴BD=AE.
点评 本题考查了等边三角形的性质,三角形外角的性质,全等三角形的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
9. 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )
如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE=80°,则∠BOD=( )| A. | 45° | B. | 80° | C. | 100° | D. | 160° |

 已知:如图,AB=AD,AC=AE,且BA⊥AC,DA⊥AE.求证:
已知:如图,AB=AD,AC=AE,且BA⊥AC,DA⊥AE.求证: