题目内容
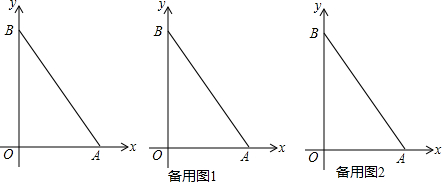
3. 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=$\frac{m}{x}$的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(-6,-1),DE=3.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=$\frac{m}{x}$的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(-6,-1),DE=3.(1)求反比例函数与一次函数的解析式.
(2)根据图象直接回答:当x为何值时,一次函数的值小于反比例函数的值.
分析 (1)先由点C的坐标求出反比例函数的关系式,再由DE=3,求出点D的坐标,把点C,点D的坐标代入一次函数关系式求出k,b即可求一次函数的关系式.
(2)由图象可知:一次函数的值小于反比例函数的值.
解答 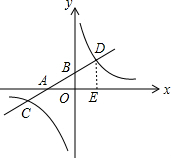 解:(1)点C(-6,-1)在反比例函数y=$\frac{m}{x}$的图象上,
解:(1)点C(-6,-1)在反比例函数y=$\frac{m}{x}$的图象上,
∴m=-6×(-1)=6,
∴反比例函数的关系式为y=$\frac{6}{x}$,
∵点D在反比例函数y=$\frac{6}{x}$上,且DE=3,
∴y=3,代入求得:x=2,
∴点D的坐标为(2,3).
∵C、D两点在直线y=kx+b上,
∴$\left\{\begin{array}{l}{2k+b=3}\\{-6k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴一次函数的关系式为y=$\frac{1}{2}$x+2.
(2)由图象可知:当x<-6或0<x<2时,一次函数的值小于反比例函数的值.
点评 本题主要考查了反比例函数与一次函数的交点,解题的关键是利用坐标解出函数的解析式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
14.抛物线y=-5(x-2)2+3的顶点坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
13.甲、乙两名队员在相同的条件下各射击10次,每次命中的环数如下表所示:
(1)甲、乙两名队员的射击成绩的平均成绩相等,请补齐甲的成绩;
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲 | 8 | 6 | 7 | 8 | 9 | 10 | 6 | 5 | 4 | 7 |
| 乙 | 7 | 9 | 8 | 5 | 6 | 7 | 7 | 6 | 7 | 8 |
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
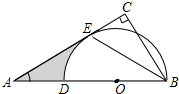 如图,在△ABC中,∠C=90°,D在AB边上,以BD为直径的半圆与AC相切于点E,连接BE.
如图,在△ABC中,∠C=90°,D在AB边上,以BD为直径的半圆与AC相切于点E,连接BE. 已知P(5,5),点B、A分别在x的正半轴和y的正半轴上,∠APB=90°,则OA+OB=10.
已知P(5,5),点B、A分别在x的正半轴和y的正半轴上,∠APB=90°,则OA+OB=10.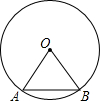 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.
如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.