题目内容
13.因式分解:(1)m(a-3)+2(3-a);
(2)2(1-x)2+6a(x-1)2;
(3)(2x+y)2-(x+2y)2;
(4)(p-4)(p+1)+3p
(5)4xy2-4x2y-y3;
(6)(m+n)2-4m(m+n)+4m2.
分析 (1)利用提公因式法,进行因式分解;
(2)利用提公因式法,进行因式分解;
(3)利用平方差公式,进行因式分解;
(4)利用平方差公式,进行因式分解;
(5)利用提公因式法和完全平方公式,进行因式分解;
(6)利用完全平方公式,进行因式分解.
解答 解:(1)m(a-3)+2(3-a)
=m(a-3)-2(a-3)
=(a-3)(m-2)
(2)2(1-x)2+6a(x-1)2
=2(x-1)2+6a(x-1)2
=2(x-1)2(1+3a)
(3))(2x+y)2-(x+2y)2
=[(2x+y)+(x+2y)][(2x+y)-(x+2y)]
=[3x+3y)][x-y)]
=3(x+y)(x-y)
(4)(p-4)(p+1)+3p
=p2-3p-4+3p
=p2-4
=(p+2)(p+2).
(5)4xy2-4x2y-y3;
=-y(4x2-4xy+y2)
═-y(2x-y)2
(6)(m+n)2-4m(m+n)+4m2.
=(m+n)2-2•(m+n)•2m+(2m)2
=[(m+n)-2m]2.
点评 本题考查了因式分解,解决本题的关键是掌握因式分解的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
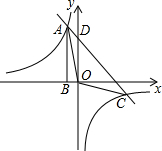 如图,点A是反比例函数$y=\frac{k}{x}({k<0})$图象上的一点,过点A作AB⊥x轴于点B,且△AOB的面积为2,点A的坐标为(-1,m).
如图,点A是反比例函数$y=\frac{k}{x}({k<0})$图象上的一点,过点A作AB⊥x轴于点B,且△AOB的面积为2,点A的坐标为(-1,m). 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=$\frac{m}{x}$的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(-6,-1),DE=3.
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=$\frac{m}{x}$的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(-6,-1),DE=3.