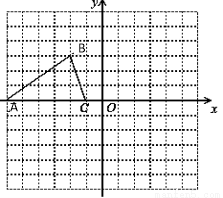
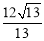题目内容
图1和图2中,优弧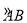 所在⊙O的半径为2,AB=2
所在⊙O的半径为2,AB=2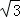 .点P为优弧
.点P为优弧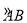 上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
上一点(点P不与A,B重合),将图形沿BP折叠,得到点A的对称点A′.
(1)点O到弦AB的距离是 ,当BP经过点O时,∠ABA′= °;
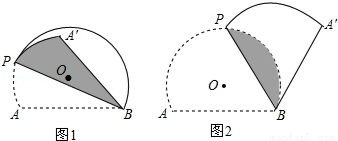
(2)当BA′与⊙O相切时,如图2,求折痕的长:
(3)若线段BA′与优弧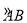 只有一个公共点B,设∠ABP=α.确定α的取值范围.
只有一个公共点B,设∠ABP=α.确定α的取值范围.
(1)1、60.(2)2 ;(3)α的取值范围是0°<α<30°或60°≤α<120°.
;(3)α的取值范围是0°<α<30°或60°≤α<120°.
【解析】
试题分析:(1)利用垂径定理和勾股定理即可求出点O到AB的距离;利用锐角三角函数的定义及轴对称性就可求出∠ABA′.
(2)根据切线的性质得到∠OBA′=90°,从而得到∠ABA′=120°,就可求出∠ABP,进而求出∠OBP=30°.过点O作OG⊥BP,垂足为G,容易求出OG、BG的长,根据垂径定理就可求出折痕的长.
(3)根据点A′的位置不同,分点A′在⊙O内和⊙O外两种情况进行讨论.点A′在⊙O内时,线段BA′与优弧 都只有一个公共点B,α的范围是0°<α<30°;当点A′在⊙O的外部时,从BA′与⊙O相切开始,以后线段BA′与优弧
都只有一个公共点B,α的范围是0°<α<30°;当点A′在⊙O的外部时,从BA′与⊙O相切开始,以后线段BA′与优弧 都只有一个公共点B,α的范围是60°≤α<120°.从而得到:线段BA′与优弧
都只有一个公共点B,α的范围是60°≤α<120°.从而得到:线段BA′与优弧 只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
试题解析:(1)①过点O作OH⊥AB,垂足为H,连接OB,如图1①所示.
∵OH⊥AB,AB=2 ,
,
∴AH=BH= .
.
∵OB=2,
∴OH=1.
∴点O到AB的距离为1.
②当BP经过点O时,如图1②所示.
∵OH=1,OB=2,OH⊥AB,
∴sin∠OBH=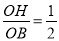 .
.
∴∠OBH=30°.
由折叠可得:∠A′BP=∠ABP=30°.
∴∠ABA′=60°.
(2)过点O作OG⊥BP,垂足为G,如图2所示.
∵BA′与⊙O相切,
∴OB⊥A′B.
∴∠OBA′=90°.
∵∠OBH=30°,
∴∠ABA′=120°.
∴∠A′BP=∠ABP=60°.
∴∠OBP=30°.
∴OG=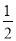 OB=1.
OB=1.
∴BG= .
.
∵OG⊥BP,
∴BG=PG= .
.
∴BP=2 .
.
∴折痕的长为2 .
.
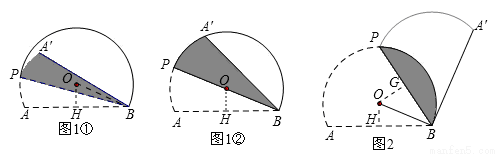
(3)若线段BA′与优弧 只有一个公共点B,
只有一个公共点B,
Ⅰ.当点A′在⊙O的内部时,此时α的范围是0°<α<30°.
Ⅱ.当点A′在⊙O的外部时,此时α的范围是60°≤α<120°.
综上所述:线段BA′与优弧 只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
只有一个公共点B时,α的取值范围是0°<α<30°或60°≤α<120°.
考点:圆的综合题.

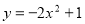 的图像上有两点P1(x1,y1),P2(x2,y2),当0<x1 <x2 时,
的图像上有两点P1(x1,y1),P2(x2,y2),当0<x1 <x2 时,  ,则cosA等于( ).
,则cosA等于( ).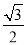 B.
B.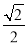 C.
C. D.1
D.1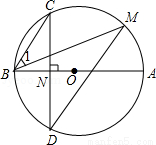
 ,求⊙O的直径.
,求⊙O的直径.
 ,则BC的长为( )
,则BC的长为( ) C.
C.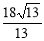 D.
D.