��Ŀ����
����С������12�֣������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ���������������ν������������Σ�
��1�����ݡ����������Ρ��Ķ��壬�����ж����⡰�ȱ�������һ�������������Ρ���������Ǽ�����?
��2����Rt��ABC�У���ACB=90�㣬AB=c��AC=b��BC=a����b>a����Rt��ABC�����������Σ���a��b��c��
��3����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣨�����A��B�غϣ���D�ǰ�Բ ���е㣬C��D��ֱ��AB�����࣬���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
���е㣬C��D��ֱ��AB�����࣬���ڡ�O�ڴ��ڵ�E��ʹAE=AD��CB=CE��

����֤����ACE�����������Σ�
�ڵ���ACE��ֱ��������ʱ�����AOC�Ķ�����
��1�������⣮��2��a��b��c=1�� ��
�� ����3���ټ�������60���120�㣮
����3���ټ�������60���120�㣮
��������
�����������1����ȱ������εı߳�Ϊa��������鼴�ɣ���2����Rt��ABC�У��ɹ��ɶ����ɵ�
a2+b2=c2�٣���ΪRt��ABC�����������Σ���b��a������a2+c2=2b2�ڣ�Ȼ��ɵ�b= a��c=
a��c= a���������3����Ҫ֤����ACE�����������Σ�ֻ��֤AC2+CE2=2AE2���ɣ����ɢٿɵæ�ACE�����������Σ�����AC2+CE2=2AE2�� ����ACE��ֱ��������ʱ���ɣ�2���ɵ�AC��AE��CE=1��
a���������3����Ҫ֤����ACE�����������Σ�ֻ��֤AC2+CE2=2AE2���ɣ����ɢٿɵæ�ACE�����������Σ�����AC2+CE2=2AE2�� ����ACE��ֱ��������ʱ���ɣ�2���ɵ�AC��AE��CE=1�� ��
�� ��AC��AE��CE=
��AC��AE��CE= ��
�� �� 1��Ȼ��������������.
�� 1��Ȼ��������������.
�����������������
��1�������⣮ ��2�֣�
��2����Rt��ABC��a2+b2=c2��
��c>b>a>0����2c2>a2+b2��2a2<b2+c2��
����ABC�����������Σ�һ����2b2=a2+c2�� ��3�֣�
��2b2=a2+��a2+b2������b2=2a2����b= a��
a��
��c2=b2+a2=3a2����c= a��
a��
��a��b��c=1�� ��
�� �� ��5�֣�
�� ��5�֣�
��3����Rt��ABC��a2+b2=c2��
��֤������AB�ǡ�O��ֱ�������ACB=��ADB=90�㣬
��Rt��ACB��AC2+BC2=AB2��
��Rt��ADB��AD2+BD2=AB2��
��D�ǰ�Բ ���е㣬��
���е㣬�� ��
��
��AD=BD�� ��6�֣���
��AB2=AD2+BD2=2AD2�� ��7�֣�
�֡�CB=CE��AE=AD����AC2+CE2=2AE2��
�তACE�����������Σ� ��8�֣�
���ɢٿɵæ�ACE�����������Σ���AC2+CE2=2AE2��
����ACE��ֱ��������ʱ��
�ɣ�2���ɵ�AC��AE��CE=1�� ��
�� ��AC��AE��CE=
��AC��AE��CE= ��
�� �� 1��
�� 1��
����AC��AE��CE=1�� ��
�� ʱ��
ʱ��
AC��CE=1�� ����AC��CB=1��
����AC��CB=1�� ��
��
�ߡ�ACB=900�������ABC=30�㣬
���AOC=2��ABC=60�㣮 ��10�֣�

����AC��AE��CE= ��
�� ��1ʱ��
��1ʱ��
AC��CE= ��1����AC��CB=
��1����AC��CB= ��1��
��1��
�ߡ�ACB=90�㣬���ABC=60�㣬
���AOC=2��ABC=120�㣬
���AOC�Ķ���Ϊ60���120�㣮 ��12�֣�
���㣺1.���⣻2.���ɶ�����3.Բ�ܽǶ��������ۣ�4.ֱ�������ε�����.

 ��У����ϵ�д�
��У����ϵ�д� A
A A
A �������������εĽ����ߡ�������
�������������εĽ����ߡ������� ��
�� ��
�� ����Բ�������ǵ�B��C��D��Aѭ�������A
����Բ�������ǵ�B��C��D��Aѭ�������A �������� .
�������� .
 �˶������ص���M��λ�á����P�˶���·��Ϊx��P��M����֮��ľ���Ϊy����ͼ������ǣ� ����
�˶������ص���M��λ�á����P�˶���·��Ϊx��P��M����֮��ľ���Ϊy����ͼ������ǣ� ����


 x2+bx������A��4��0�������C��1��-3�������������ߵĶԳ�����ȷ��һ��D��ʹ��
x2+bx������A��4��0�������C��1��-3�������������ߵĶԳ�����ȷ��һ��D��ʹ�� ��ֵ�����D�������Ϊ_____��
��ֵ�����D�������Ϊ_____��
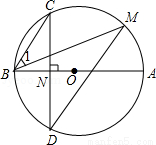
 �����O��ֱ����
�����O��ֱ����