题目内容
16.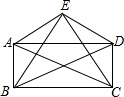 如图,平行四边形ABCD中,以对角线AC为斜边作Rt△ACE,又∠BED=90°,那么平行四边形ABCD是矩形吗?说说你的理由.
如图,平行四边形ABCD中,以对角线AC为斜边作Rt△ACE,又∠BED=90°,那么平行四边形ABCD是矩形吗?说说你的理由.
分析 连接EO,首先根据平行四边形的性质可得AO=CO,BO=DO,即O为BD和AC的中点,在Rt△AEC中EO=$\frac{1}{2}$AC,在Rt△EBD中,EO=$\frac{1}{2}$BD,进而得到AC=BD,再根据对角线相等的平行四边形是矩形可证出结论.
解答 证明:平行四边形ABCD是矩形;
连接EO,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,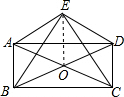
在Rt△EBD中,
∵O为BD中点,
∴EO=$\frac{1}{2}$BD,
在Rt△AEC中,∵O为AC中点,
∴EO=$\frac{1}{2}$AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,关键是掌握直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
4.下列说法中,正确的是( )
| A. | 两条射线组成的图形叫做角 | |
| B. | 有公共端点的两条线段组成的图形叫做角 | |
| C. | 角可以看做是由一条射线绕着它的端点旋转而形成的图形 | |
| D. | 角可以看做是由一条线段绕着它的端点旋转而形成的图形 |
11. 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )| A. | 64m2 | B. | 32m2 | C. | 128m2 | D. | 96m2 |

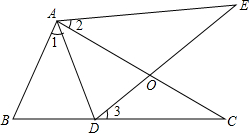 如图,∠1=∠2=∠3,AB=AD,请说明BC=DE.
如图,∠1=∠2=∠3,AB=AD,请说明BC=DE.