题目内容
11.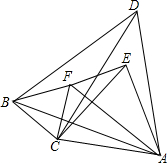 如图所示,平面上三个正三角形ACE,△ABD,△BCF两两共有一个顶点,求证:CD与EF互相平分.
如图所示,平面上三个正三角形ACE,△ABD,△BCF两两共有一个顶点,求证:CD与EF互相平分.
分析 首先连接DE、DF,由△CBF和△ABD是等边三角形,易证得△CBA≌△FBD(SAS),继而证得AC=DF,则可得DF=EC,同理可得DE=FC,则可判定四边形DECF是平行四边形,证得CD与EF互相平分.
解答 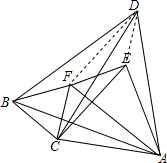 证明:如图,连接DE、DF,
证明:如图,连接DE、DF,
∵△CBF和△ABD是等边三角形,
∴CB=FB,BA=BD,∠ABD=∠CBF=60°,
∵∠CBA=60°-∠ABF,∠FBD=60°-∠ABF,
∴∠CBA=∠FBD,
在△CBA和△FBD中,
$\left\{\begin{array}{l}{CB=FB}\\{∠CBA=∠FBD}\\{BA=BD}\end{array}\right.$,
∴△CBA≌△FBD(SAS),
∴AC=DF,
又∵EC=AC,
∴DF=EC,
同理可得:DE=FC,
∴四边形DECF是平行四边形,
∴CD与EF互相平分.
点评 此题考查了平行四边形的判定与性质以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
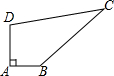 如图所示,一块四边形土地ABCD,∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m,求四边形土地ABCD的面积.
如图所示,一块四边形土地ABCD,∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m,求四边形土地ABCD的面积.