题目内容
4.将下列各式通分(1)$\frac{3}{{a}^{2}b}$与$\frac{2}{2ab}$;
(2)$\frac{a}{a+b}$与$\frac{b}{a-b}$.
分析 (1)先确定最简公分母为2a2b,然后根据分式的基本性质把分母化为同分母;
(2)先确定最简公分母为(a+b)(a-b),然后根据分式的基本性质把分母化为同分母.
解答 解:(1)最简公分母是:2a2b,
$\frac{3}{{a}^{2}b}$=$\frac{6}{2{a}^{2}b}$,$\frac{2}{2ab}$=$\frac{2a}{2{a}^{2}b}$;
(2)最简公分母是:(a+b)(a-b),
$\frac{a}{a+b}=\frac{a(a-b)}{(a+b)(a-b)}$;
$\frac{b}{a-b}=\frac{b(a+b)}{(a+b)(a-b)}$.
点评 本题主要考查通分,通分的关键是确定最简公分母,属基础题.

练习册系列答案
相关题目
14.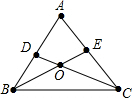 如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )| A. | 120° | B. | 60° | C. | 150° | D. | 不能确定 |
19.已知线段AB=6cm,在直线AB上画线BC,使BC=11cm,则线段AC=( )
| A. | 17cm | B. | 5cm | C. | 11cm或5cm | D. | 5cm或17cm |
 如图△ABC中,D在AB上,E在AC上,CD与BE交于F点,DF=CF,BD=2AD,求$\frac{BF}{EF}$,$\frac{AE}{CE}$.
如图△ABC中,D在AB上,E在AC上,CD与BE交于F点,DF=CF,BD=2AD,求$\frac{BF}{EF}$,$\frac{AE}{CE}$.