题目内容
14.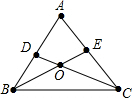 如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于O,∠A=60°,则∠BOC的度数是( )| A. | 120° | B. | 60° | C. | 150° | D. | 不能确定 |
分析 先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由角平分线的性质得出∠OBC+∠OCB的度数,由三角形内角和定理即可得出结论.
解答 解:∵在△ABC中,∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×120°=60°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-60°=120°.
故选A.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
4.一元二次方程x=x(x-2)的根是( )
| A. | 0或2 | B. | 0或3 | C. | 1或2 | D. | 3 |
2.已知a=2x,b=2y,x+y=100xy,那么分式$\frac{a+b}{ab}$的值等于( )
| A. | 200 | B. | 100 | C. | 50 | D. | 25 |
19.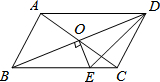 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )| A. | 8cm | B. | 12cm | C. | 16cm | D. | 24cm |
 如图,在高3米,坡面线段AB长为5米的楼梯表面铺地毯,已知楼梯宽1.5米,地毯售价为40元/平方米,若将楼梯表面铺满地毯,则至少需420元.
如图,在高3米,坡面线段AB长为5米的楼梯表面铺地毯,已知楼梯宽1.5米,地毯售价为40元/平方米,若将楼梯表面铺满地毯,则至少需420元.
 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A2,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A2,得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )