题目内容
11.若$\sqrt{{(a-1)}^{2}}$+$\sqrt{{a}^{2}}$=1-2a,求|1-a|-|a|的值.分析 根据二次根式的性质得出a的取值范围,再利用绝对值的定义化简解答即可.
解答 解:因为$\sqrt{{(a-1)}^{2}}$+$\sqrt{{a}^{2}}$=1-2a,
可得:a≤0,
所以当a=0时,|1-a|-|a|=1-a-a=1-2a=1,
当a<0时,|1-a|-|a|=1-a+a=1.
点评 此题考查二次根式的化简,关键是根据二次根式的性质得出a的取值范围.

练习册系列答案
相关题目
16.若(x+4)(x-5)=x2+mx+n,则m+n=( )
| A. | 21 | B. | -21 | C. | 19 | D. | -19 |
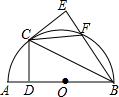 如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.
如图,以AB为直径作半圆O,点C为半圆上与A,B不重合的一动点,过点C作CD⊥AB于点D,点E与点D关于BC对称,BE与半圆交于点F,连CE.