题目内容
16. 某水果销售店在试销售成本为每千克2元的某种水果,规定试销期间销售单价不低于成本单价,也不高于每千克4元.经试销发现,每天的销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
某水果销售店在试销售成本为每千克2元的某种水果,规定试销期间销售单价不低于成本单价,也不高于每千克4元.经试销发现,每天的销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.(1)求y与x的函数解析式;
(2)设水果销售店试销该种水果期间每天获得的利润为W元,求W的最大值.
分析 (1)根据图象中的数据可以求得y与x的函数解析式;
(2)根据题意可以得到W与x的函数关系式,然后将函数关系式化为顶点式,再根据x的取值范围即可求得W的最大值.
解答 解:(1)设y与x的函数关系式为y=kx+b,
则$\left\{\begin{array}{l}2k+b=300\\ 3k+b=280\end{array}\right.$,
解得,$\left\{\begin{array}{l}k=-20\\ b=340\end{array}\right.$,
∴y与x的函数解析式为y=-20x+340,(2≤x≤4);
(2)由已知得,
W=(x-2)(-20x+340)=-20(x-9.5)2+1125,
∵-20<0,
∴当x≤9.5时,W随x的增大而增大,
∵2≤x≤4,
∴当x=4时,W取得最大值,此时W=-20(4-9.5)2+1125=520,
即W的最大值520.
点评 本题考查二次函数的应用,解答此类问题的关键是明确题意,求出相应的函数解析式,利用二次函数的顶点式和自变量的取值范围求函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠ADC=33°,则∠ACB等于( )| A. | 57° | B. | 66° | C. | 67° | D. | 44° |
11.如图,点O是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使$\widehat{AB}$和$\widehat{BC}$都经过圆心O,已知⊙O的半径为3,则阴影部分的面积是( )
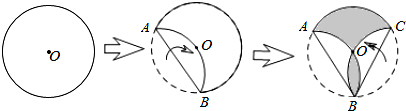

| A. | $\frac{9}{4}π$ | B. | $\frac{9}{2}π$ | C. | 2π | D. | 3π |
1.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2+a3=a5 | C. | a2•a3=a5 | D. | a5÷a5=0 |
 (1)已知⊙O的直径为6,圆心O到直线l的距离为5,
(1)已知⊙O的直径为6,圆心O到直线l的距离为5, 如图,⊙O的半径为2,∠OAB=30°,AB切⊙O于B,弦BC∥OA,连结AC.则图中阴影部分的面积S=$\frac{2π}{3}$.
如图,⊙O的半径为2,∠OAB=30°,AB切⊙O于B,弦BC∥OA,连结AC.则图中阴影部分的面积S=$\frac{2π}{3}$. 如图,在等腰△ABC中,AB=AC,∠A=40°,AB的垂直垂直平分线DE交AB于点D,交BC于点E,则∠EBC=30°.
如图,在等腰△ABC中,AB=AC,∠A=40°,AB的垂直垂直平分线DE交AB于点D,交BC于点E,则∠EBC=30°.