题目内容
16. 如图,在四边形ABCD中,AB=CD,AD=BC,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.
如图,在四边形ABCD中,AB=CD,AD=BC,E是CA延长线上的点,F是AC延长线上的点,且AE=CF.(1)△ABE与△CDF全等吗?请说明理由.
(2)BE与DF有什么关系?请说明理由.
分析 (1)先证明四边形ABCD是平行四边形,得出AB∥CD,由平行线的性质得出∠BAC=∠DCA,得出∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由全等三角形的性质即可得出结论.
解答 解:(1)△ABE≌△CDF;理由如下:
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠DCA,
∴∠BAE=∠DCF,
在△ABE和△CDF中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠BAE=∠DCF}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SAS);
(2)BE=DF;理由如下:
∵△ABE≌△CDF,
∴BE=DF.
点评 此题考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
4. 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表
请回答下列问题:
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
(1)将各岗位人数统计图补充完整;
(2)求该公司服务员每人的基本工资;
(3)该公司所有员工基本工资的中位数是1500元,众数是1400元;你认为用基本工资的平均数和中位数来代表该公司员工基本工资的一般水平,哪一个更恰当?请说明理由.
 已知:如图,AB∥CD,∠B=∠D,求证:△ABC≌△CDA.
已知:如图,AB∥CD,∠B=∠D,求证:△ABC≌△CDA.
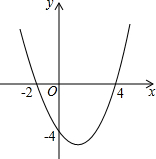 二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题:
二次函数y=ax2+bx+c的图象如图所示,根据图象回答下列问题: