题目内容
18.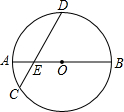 如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.
如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.(1)已知CE=6,DE=10,求AB的长;
(2)记CE=m,DE=n,求$\frac{C{E}^{2}+D{E}^{2}}{A{B}^{2}}$的值.
分析 (1)作OF⊥CD于F,连接OD,由垂径定理得出FD=CF=$\frac{1}{2}$CD,求出EF的长,证得△EFO为等腰直角三角形,得出OF=EF=2,由勾股定理求得OD的长,即可求得AB的长;(2)同(1)求出FD=CF=$\frac{1}{2}$CD、EF=CF-CE、OF、OD的长,代入即可得出结果.
解答 解:(1)作OF⊥CD于F,连接OD,如图所示:
∵CE=6,DE=10,
∴CD=16,
由垂径定理得:FD=CF=$\frac{1}{2}$CD=8,
∴EF=CF-CE=8-6=2,
∵∠DEB=45°,
∴△EFO为等腰直角三角形,
∴OF=EF=2,
由勾股定理得:OD=$\sqrt{O{F}^{2}+F{D}^{2}}$=$\sqrt{{2}^{2}+{8}^{2}}$=2$\sqrt{17}$,
∴AB=2OD=2×2$\sqrt{17}$=4$\sqrt{17}$;
(2)∵CE=m,DE=n,
∴CD=m+n,
由垂径定理得:FD=CF=$\frac{1}{2}$CD,EF=CF-CE=$\frac{1}{2}$(m+n)-m=$\frac{n-m}{2}$,
∴OF=$\frac{n+m}{2}$,
∴OD=$\sqrt{D{F}^{2}+O{F}^{2}}$=$\sqrt{(\frac{m+n}{2})^{2}+(\frac{n-m}{2})^{2}}$=$\sqrt{\frac{{m}^{2}+{n}^{2}}{2}}$,
∴$\frac{C{E}^{2}+D{E}^{2}}{A{B}^{2}}$=$\frac{{m}^{2}+{n}^{2}}{(2OD)^{2}}$=$\frac{{m}^{2}+{n}^{2}}{(2×\sqrt{\frac{{m}^{2}+{n}^{2}}{2}})^{2}}$=$\frac{{m}^{2}+{n}^{2}}{2({m}^{2}+{n}^{2})}$=$\frac{1}{2}$.
点评 本题考查了垂径定理、等腰直角三角形的判定与性质、勾股定理;熟练掌握垂径定理,运用勾股定理进行计算是解决问题的关键,本题有一定难度.

 阅读快车系列答案
阅读快车系列答案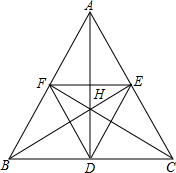 如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )
如图,锐角△ABC的垂心为H,三条高的垂足分为D、E、F,则H是△DEF的( )| A. | 垂心 | B. | 重心 | C. | 内心 | D. | 外心 |

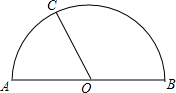 如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5.
如图,在以AB为直径的半圆中,半径OC=4,且S扇形AOC:S扇形BOC=3:5. 如图,?ABCD中,AE平分∠DAB,∠B=100°,则∠DAE等于40°.
如图,?ABCD中,AE平分∠DAB,∠B=100°,则∠DAE等于40°.