题目内容
10.如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点且△OCD的面积为$\frac{5}{2}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点D且与边BA交于点E,连接DE.(1)反比例函数的表达式为y=$\frac{5}{x}$;
(2)在x轴上是否存在一点P,使得S△POB=$\frac{1}{3}$S矩形OABC;
(3)若线段MN=1在x轴移动(M在N的左边),求四边形DMNE周长最短时点M的坐标.

分析 (1)要求反比例函数的表达式,只需求出点D的坐标即可;
(2)如图1,要求点P的坐标,只需求出OP即可;
(3)由于DE、MN的长度是定值,要使四边形DMNE周长最短,只需DM+EN最小,可将DM向右平移1个单位到D′N,只需D′N+NE最短,延长EA到点E′,使得AE′=AE,则有NE′=NE,只需D′N+NE′最短,根据两点之间线段最短可得:当D′、N、E′共线时,D′N+NE′最短,易证△E′AN∽△E′BD′,利用相似三角形的性质可求出AN,从而可求出OM,即可得到点M的坐标.
解答 解:(1)∵S△OCD=$\frac{1}{2}$OC•CD=$\frac{5}{2}$,OC=5,∴CD=1,
∴点D的坐标为(1,5).
∵点D在反比例函数y=$\frac{k}{x}$的图象上,
∴k=1×5=5,
∴反比例函数的解析式为y=$\frac{5}{x}$.
故答案为y=$\frac{5}{x}$;
(2)如图1,
∵S△POB=$\frac{1}{3}$S矩形OABC,
∴$\frac{1}{2}$OP×5=$\frac{1}{3}$×3×5,
∴OP=2,
∴点P的坐标为(2,0)或(-2,0);
(3)延长EA到点E′,使得AE′=AE,在DB上取一点D′,使得DD′=1,
连接D′E′,交OA于N,如图2,
∵四边形OABC是矩形,
∴BC∥OA,∠OAB=90°,
∴DD′∥MN,NE′=NE.
∵DD′=MN=1,
∴四边形DD′NM是平行四边形,
∴D′N=DM.
根据两点之间线段最短可得:
此时DM+EN=D′N+EN=D′N+NE′最短,
由于DE、MN的长度是定值,
因此此时四边形DMNE周长最短.
∵xE=3,∴yE=$\frac{5}{3}$,
∴AE=$\frac{5}{3}$,
∴AE′=$\frac{5}{3}$,E′B=$\frac{5}{3}$+5=$\frac{20}{3}$,
∴$\frac{AE′}{E′B}$=$\frac{1}{4}$.
∵AN∥BC,
∴△E′AN∽△E′BD′,
∴$\frac{AN}{BD′}$=$\frac{E′A}{E′B}$,
∴$\frac{AN}{3-1-1}$=$\frac{1}{4}$,
∴AN=$\frac{1}{4}$,
∴OM=3-1-$\frac{1}{4}$=$\frac{7}{4}$,
∴点M的坐标为($\frac{7}{4}$,0).
点评 本题主要考查了运用待定系数法求反比例函数的解析式、矩形的性质、平行四边形的判定与性质、相似三角形的判定与性质、两点之间线段最短等知识,将不相连的两条线段和最短转化为相连的两条线段和最短,是解决第(3)小题的关键.

| A. | 0 | B. | 1$\frac{1}{8}$ | C. | -1$\frac{1}{8}$ | D. | $\frac{1}{2}$ |
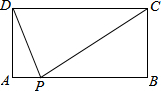 如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.
如图,矩形ABCD中,AB=5,AD=2,点P是AB边上不与A、B重合的点,要使△DPA与△PCB相似(相似比不为1),需加一个条件,这个条件是∠DPC=90°.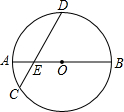 如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.
如图,⊙O的直径AB和弦CD相交于点E,∠DEB=45°.