题目内容
3. 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.
分析 连接PM、PN,如图,根据切线长定理得PM⊥x轴,PN⊥y轴于N,则PM=PN=1,再利用等角的余角相等得∠1=∠3,则可证明△PMF≌△PNE,于是有MF=NE,即b-1=a+1,所以b=a+2.
解答 解:连接PM、PN,如图
∵⊙P与x轴,y轴分别相切于点M和点N,
∴PM⊥x轴,PN⊥y轴于N,
而P(1,1),
∴PM=1,PN=1,
∵PE⊥PF,
∴∠1+∠2=90°,
∵∠3+∠2=90°,
∴∠1=∠3,
在△PMF和△PNE
$\left\{\begin{array}{l}{∠1=∠3}\\{PM=PN}\\{∠PMF=∠PNE}\end{array}\right.$,
∴△PMF≌△PNE,
∴MF=NE,
即b-1=a+1,
∴b=a+2.
故答案为b=a+2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.由定理可知,若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.也考查了坐标与图形性质.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13.在平面直角坐标系中,点P(-2,a)与点Q(b,3)关于原点对称,则a+b的值为( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
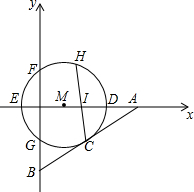 如图,直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$与x轴、y轴分别交于点A,B两点.点M为x轴上一点,以M为圆心,2为半径作圆,⊙M恰好与直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$相切,切点为C.设⊙M与x轴、y轴分别交于D、E、G、F,H为⊙M上一点,连结HC交x轴于点I.给出下列结论:①OA=5;②∠BAO=30°;③点M的坐标为(1,0);④CD=2;⑤若EI:IC=3:2,则cos∠HCD=$\frac{3}{5}$.其中正确的有①②③④.
如图,直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$与x轴、y轴分别交于点A,B两点.点M为x轴上一点,以M为圆心,2为半径作圆,⊙M恰好与直线y=$\frac{\sqrt{3}}{3}$x-$\frac{5\sqrt{3}}{3}$相切,切点为C.设⊙M与x轴、y轴分别交于D、E、G、F,H为⊙M上一点,连结HC交x轴于点I.给出下列结论:①OA=5;②∠BAO=30°;③点M的坐标为(1,0);④CD=2;⑤若EI:IC=3:2,则cos∠HCD=$\frac{3}{5}$.其中正确的有①②③④.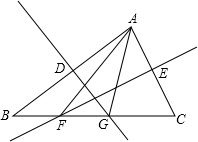 如图,直线DG和EF分别是△ABC的边AB、AC的垂直平分线,它们与BC的交点分别是G、F点,∠B=35°,∠C=65°,求∠FAG的度数.
如图,直线DG和EF分别是△ABC的边AB、AC的垂直平分线,它们与BC的交点分别是G、F点,∠B=35°,∠C=65°,求∠FAG的度数.