题目内容
8.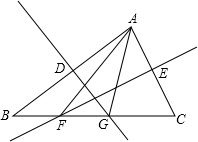 如图,直线DG和EF分别是△ABC的边AB、AC的垂直平分线,它们与BC的交点分别是G、F点,∠B=35°,∠C=65°,求∠FAG的度数.
如图,直线DG和EF分别是△ABC的边AB、AC的垂直平分线,它们与BC的交点分别是G、F点,∠B=35°,∠C=65°,求∠FAG的度数.
分析 根据三角形内角和定理求出∠BAC的度数,根据线段的垂直平分线的性质得到AG=BGAF=CF,根据等腰三角形的性质分别求出∠CAG和∠BAF的度数,计算得到∠FAG的度数.
解答 解:∵∠B=35°,∠C=65°,
∴∠BAC=80°,
∵DG是线段AB的垂直平分线,
∴AG=BG,
∴∠DAG=∠B=35°,
∴∠GAC=45°,
∵EF是线段AC的垂直平分线,
∴FA=FC,
∴∠EAF=∠C=65°,
∴∠BAF=15°,
∴∠FAG=∠BAC-∠BAF-∠CAG=20°.
点评 本题考查的是线段的垂直平分线的性质和三角形内角和定理的应用,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
18.下列各数,立方根一定是负数的是( )
| A. | -a | B. | -a2 | C. | -a2-1 | D. | -a2+1 |
13.若方程(m-1)${x^{{m^2}+1}}$-x+3=0是关于x的一元二次方程,那么m的值为( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 以上都不对 |
17.下列实数中,是有理数的为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{4}$ | C. | π | D. | 0 |
 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.
已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0).在点F运动过程中,设OE=a,OF=b,用含a的代数式表示b为b=a+2.