题目内容
3.若2m=3n,则下列比例式中不正确的是( )| A. | $\frac{m}{n}=\frac{3}{2}$ | B. | $\frac{m}{3}=\frac{n}{2}$ | C. | $\frac{m}{2}=\frac{n}{3}$ | D. | $\frac{2}{n}=\frac{3}{m}$ |
分析 根据比例的性质内项之积等于外项之积,即可判断.
解答 解:∵2m=3n,
∴$\frac{m}{n}$=$\frac{3}{2}$或$\frac{m}{3}$=$\frac{n}{2}$或$\frac{2}{n}$=$\frac{3}{m}$,
故选C.
点评 本题考查比例的性质,记住比例的性质内项之积等于外项之积是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.无理数$\sqrt{31}$的整数部分是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
18.绝对值大于π而不大于6的所有正整数之和为( )
| A. | 0 | B. | 9 | C. | 10 | D. | 15 |
8.等腰三角形的两边长为1和3,则周长为( )
| A. | 7 | B. | 5 | C. | 7或5 | D. | 无法确定 |
13.方程2x2-4x+1=0化成(x+m)2=n(n≥0)的形式是( )
| A. | (x-1)2=$\frac{1}{2}$ | B. | (2x-1)2=$\frac{1}{2}$ | C. | (x-1)2=0 | D. | (x-2)2=3 |
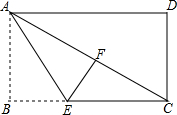 如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为( )
如图,在矩形纸片ABCD中,AB=6,AD=8,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则线段EF的长为( )
 如图,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AC的中点,DE的延长线交BC的延长线于点F,EF=5,∠B的正切值为$\frac{1}{3}$
如图,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,E是AC的中点,DE的延长线交BC的延长线于点F,EF=5,∠B的正切值为$\frac{1}{3}$