题目内容
14．
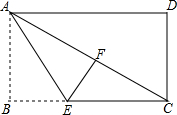如图，在矩形纸片ABCD中，AB=6，AD=8，折叠该纸片，使得AB边落在对角线AC上，点B落在点F处，折痕为AE，则线段EF的长为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 利用勾股定理列式求出AC，设BE=x，表示出CE，根据翻折的性质可得BE=EF，AF=AB，再求出CF，然后利用勾股定理列方程求出x，即可．
解答 解：由勾股定理得，AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10，
设BE=x，则CE=8-x，
由翻折的性质得，BE=EF=x，AF=AB=6，
所以，CF=10-6=4，
在Rt△CEF中，由勾股定理得，EF2+CF2=CE2，
即x2+42=（8-x）2，
解得x=3，
∴EF=3，
故选A．
点评 本题考查了翻折变换的性质，勾股定理，此类题目，熟记性质并利用勾股定理列出方程是解题的关键．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
2．下列运算正确的是（ ）
| A． | 2x+3y=5xy | B． | 5m2•m3=5m5 | C． | a6÷a3=a2 | D． | （m2）3=m5 |
9．
如图，已知点D是AB边的中点，AF∥BC，CG：GA=3：1，BC=8，则AF等于（ ）
如图，已知点D是AB边的中点，AF∥BC，CG：GA=3：1，BC=8，则AF等于（ ）| A． | 2 | B． | 4 | C． | 16 | D． | 8 |
19．实数-8，-3，-5，0中最小的数是（ ）
| A． | 0 | B． | -8 | C． | -5 | D． | -3 |
6．下列分式$\frac{a+b}{{a}^{2}+{b}^{2}}$，$\frac{3y}{15x}$，$\frac{x+y}{{x}^{2}-{y}^{2}}$，$\frac{x+1}{{x}^{2}+1}$中，最简分式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
3．若2m=3n，则下列比例式中不正确的是（ ）
| A． | $\frac{m}{n}=\frac{3}{2}$ | B． | $\frac{m}{3}=\frac{n}{2}$ | C． | $\frac{m}{2}=\frac{n}{3}$ | D． | $\frac{2}{n}=\frac{3}{m}$ |