题目内容
20.分解因式:y2-4-2xy+x2=(y-x-2)(y-x+2);-(-$\frac{1}{2}$)-83×0.1252=-$\frac{15}{2}$.分析 根据完全平方公式和平方差公式进行因式分解即可.
解答 解:y2-4-2xy+x2=(y-x)2-4=(y-x-2)(y-x+2),
-(-$\frac{1}{2}$)-83×0.1252=$\frac{1}{2}$-(8×0.125)2×8=-$\frac{15}{2}$,
故答案为(y-x-2)(y-x+2),-$\frac{15}{2}$.
点评 本题考查了因式分解,掌握平方差公式和完全平方公式是解题的关键.

练习册系列答案
相关题目
11.已知:抛物线y=-$\frac{1}{4}$(x+1)2.
(1)写出抛物线的顶点坐标;
(2)完成下表:
(3)在下面的坐标系中描点画出抛物线的图象.

(1)写出抛物线的顶点坐标;
(2)完成下表:
| x | … | -7 | -5 | -3 | -1 | 1 | 3 | 5 | … |
| y | … | -9 | -9 | -1 | 0 | -1 | -4 | -9 | … |

9.已知实数x,y满足|x-4|+$\sqrt{y-8}$=0,则以x,y的值为两边长的等腰三角形的周长为( )
| A. | 20或16 | B. | 20 | C. | 16 | D. | 以上答案均不对 |
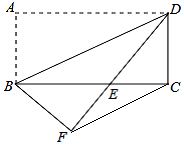 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF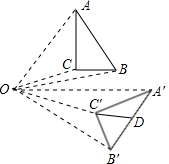 如图,Rt△ABC的斜边AB=16,Rt△ABC绕点O顺时针旋转后得到Rt△A'B'C',则Rt△A'B'C'的斜边A'B'上的中线C'D的长度为8.
如图,Rt△ABC的斜边AB=16,Rt△ABC绕点O顺时针旋转后得到Rt△A'B'C',则Rt△A'B'C'的斜边A'B'上的中线C'D的长度为8. 已知抛物线交x轴于A(-1,0),B(3,0),交y轴于C(0,-3),以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,交⊙M的切线AE于E,连接DM并延长交⊙M于N,连接AN,AD.
已知抛物线交x轴于A(-1,0),B(3,0),交y轴于C(0,-3),以AB为直径作⊙M,过抛物线上一点P作⊙M的切线PD,切点为D,交⊙M的切线AE于E,连接DM并延长交⊙M于N,连接AN,AD.