题目内容
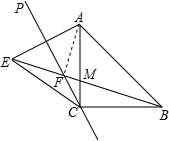 直线CP是经过等腰直角三角形ABC的直角顶点C,并且在三角形的外侧所作的直线,点A关于直线CP的对称点为E,连接BE,CE,其中BE交直线CP于点F.
直线CP是经过等腰直角三角形ABC的直角顶点C,并且在三角形的外侧所作的直线,点A关于直线CP的对称点为E,连接BE,CE,其中BE交直线CP于点F.(1)若∠PCA=25°,求∠CBF的度数.
(2)连接AF,设AC与BE的交点为点M,请判断△AFM的形状.
(3)求证:EF2+BF2=2BC2.
考点:全等三角形的判定与性质,线段垂直平分线的性质,勾股定理,等腰直角三角形
专题:综合题
分析:(1)由点A关于直线CP的对称点为E,可得△ACE是等腰三角形,结合等腰三角形和直角三角形的性质即可求得∠CBF的度数;
(2)先判定△EFC和△AFC全等,可得∠CEB=∠CAF,由等量代换可得∠FAM+∠FMA=90°,进而得出∠AFB=90°,所以△AFM是直角三角形.
(3)在直角三角形ABC和直角三角形AFB中,分别运用勾股定理,结合线段的等量代换即可得出结论.
(2)先判定△EFC和△AFC全等,可得∠CEB=∠CAF,由等量代换可得∠FAM+∠FMA=90°,进而得出∠AFB=90°,所以△AFM是直角三角形.
(3)在直角三角形ABC和直角三角形AFB中,分别运用勾股定理,结合线段的等量代换即可得出结论.
解答:解:(1)∵点A关于直线CP的对称点为E,∠PCA=25°,
∴CP是AE垂直平分线,∴FA=FE,CA=CE,∴∠ECP=∠PCA=25°,
∵△ABC为等腰直角三角形,∴CA=CB,∴CE=CB,∠CEB=∠CBE
∴∠ECB=∠ECP+∠PCA+∠ACB=25°+25°+90°=140°,
∴∠CBF=
∠ECB=
×140°=70°.
(2)在△EFC和△AFC中
,所以在△EFC和△AFC(SSS),
∴∠CEB=∠CAF,又∵∠CEB=∠CBE.
∴∠CAF=∠CBE,又∵∠CBE+∠CMB=90°,
∴∠FAM+∠CMB=90°,
∵∠CMB=∠FMA,
∴∠FAM+∠FMA=90°,
∴∠AFB=90°,
∴△AFM是直角三角形.
(3)在Rt△ABC中:AC2+BC2=AB2.
∵AC=BC.
∴AB2=2BC2.
在Rt△AFB中:AF2+BF2=AB2.
∵AF=EF,
∴EF2+BF2=AB2,
∴EF2+BF2=2BC2.
∵AF=EF,
∴EF2+BF2=AB2,
∴EF2+BF2=2BC2.
∴CP是AE垂直平分线,∴FA=FE,CA=CE,∴∠ECP=∠PCA=25°,
∵△ABC为等腰直角三角形,∴CA=CB,∴CE=CB,∠CEB=∠CBE
∴∠ECB=∠ECP+∠PCA+∠ACB=25°+25°+90°=140°,
∴∠CBF=
| 1 |
| 2 |
| 1 |
| 2 |
(2)在△EFC和△AFC中
|
∴∠CEB=∠CAF,又∵∠CEB=∠CBE.
∴∠CAF=∠CBE,又∵∠CBE+∠CMB=90°,
∴∠FAM+∠CMB=90°,
∵∠CMB=∠FMA,
∴∠FAM+∠FMA=90°,
∴∠AFB=90°,
∴△AFM是直角三角形.
(3)在Rt△ABC中:AC2+BC2=AB2.
∵AC=BC.
∴AB2=2BC2.
在Rt△AFB中:AF2+BF2=AB2.
∵AF=EF,
∴EF2+BF2=AB2,
∴EF2+BF2=2BC2.
∵AF=EF,
∴EF2+BF2=AB2,
∴EF2+BF2=2BC2.
点评:本题考查了全等三角形的性质和判定、等腰三角形的性质以及勾股定理,解决问题的关键是结合图形,熟练运用角和线段的等量代换证得结论.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
 如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是
如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是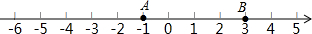 已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.
已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为x.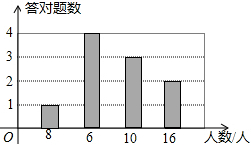 电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.
电视台在某次青年歌手大奖赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,统计结果如图所示.