题目内容
(1)解下列方程
①
-
=-2
②
-
=1,(a≠0,a≠4)
(2)化简求值:
÷(
+1),其中x=
+1.
①
| 3 |
| x-2 |
| x |
| 2-x |
②
| x+1 |
| x-1 |
| a |
| x2-1 |
(2)化简求值:
| x |
| x2-2x+1 |
| x+1 |
| x2-1 |
| 2 |
考点:分式的化简求值,解分式方程
专题:计算题
分析:(1)两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答:解:(1)①去分母得:3+x=-2x+4,
移项合并得:3x=1,
解得:x=
,
经检验x=
是分式方程的解;
②去分母得:(x+1)2-a=x2-1,
整理得:2x+1-a=-1,
解得:x=
,
∵a≠0,a≠4,
∴x≠1且x≠-1,
则x=
是分式方程的解;
(2)原式=
•
=
,
当x=
+1时,原式=
=
.
移项合并得:3x=1,
解得:x=
| 1 |
| 3 |
经检验x=
| 1 |
| 3 |
②去分母得:(x+1)2-a=x2-1,
整理得:2x+1-a=-1,
解得:x=
| a-2 |
| 2 |
∵a≠0,a≠4,
∴x≠1且x≠-1,
则x=
| a-2 |
| 2 |
(2)原式=
| x |
| (x-1)2 |
| (x+1)(x-1) |
| x(x+1) |
| 1 |
| x-1 |
当x=
| 2 |
| 1 | ||
|
| ||
| 2 |
点评:此题考查了分式的化简求值,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
当实数x的取值使得
有意义时,函数y=-4x+1中y的取值范围是( )
| x-3 |
| A、y≥-11 |
| B、y≤-11 |
| C、y≥-13 |
| D、y≤-13 |
已知,一元二次方程a(x+m)2+b=0的两根为1,2,则a(x+m-2)2+b=0的两根为( )
| A、3,4 |
| B、-1,0 |
| C、与a、m、b的值有关 |
| D、无法求出 |
若代数式m2n3x-1与3nx+3m2是同类项,则x的值为( )
| A、-1 | B、1 | C、2 | D、3 |
现在网购越来越多地成为人们的一种消费方式,刚刚过去的2014年的“双11”网上促销活动中,天猫的支付交易额突破570亿元,将570亿元用科学记数法表示为( )
| A、5.70×108 |
| B、5.70×1010 |
| C、57.0×109 |
| D、0.570×1011 |
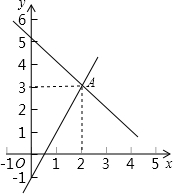 如图,点A的坐标可以看成是方程组
如图,点A的坐标可以看成是方程组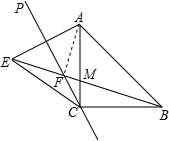 直线CP是经过等腰直角三角形ABC的直角顶点C,并且在三角形的外侧所作的直线,点A关于直线CP的对称点为E,连接BE,CE,其中BE交直线CP于点F.
直线CP是经过等腰直角三角形ABC的直角顶点C,并且在三角形的外侧所作的直线,点A关于直线CP的对称点为E,连接BE,CE,其中BE交直线CP于点F.