题目内容
4.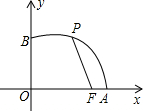 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )| A. | ①②③ | B. | ①③ | C. | ①②④ | D. | ③④ |
分析 设P的坐标是(x,y),过P作PM⊥x轴于M点,在直角△PFM中,根据勾股定理,即可求得函数的解析式.根据解析式即可判断.
解答  解:过P作PM⊥x轴于点M,如图所示:
解:过P作PM⊥x轴于点M,如图所示:
设P的坐标是(x,y).
在直角△PMF中,PM=y,MF=3-x.
∵PM2+MF2=PF2,
∴(3-x)2+y2=(5-$\frac{3}{5}$x)2,
解得:y2=-$\frac{16}{25}$x2+16.
在上式中,令y=0,解得:x=5,则AF=OA-OF=5-3=2,故①,③正确;
在上式中,令x=0,解得y=4.即OB=4.故④错误;
在直角△OBF中,根据勾股定理即可求得:BF=5,故②错误.
综上,正确的序号有①③.
故选B.
点评 本题考查了一次函数综合题,其中涉及到一次函数、二次函数的性质,勾股定理,正确作出辅助线求得函数的解析式是解决本题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
14.利用墙的一边,再用13m的铁丝,围成一个面积为20m2的长方形,求这个长方形与墙平行的一边的长.设与墙平行的一边的长为xm,可列方程为( )
| A. | ((13-x)=20 | B. | x($\frac{13-x}{2}$)=20 | C. | x(13-$\frac{1}{2}$x)=20 | D. | x($\frac{13-2x}{2}$)=20 |
 把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.
把正整数1,2,3,…,按如图所示排列.第1行第1列的数为1,第1行第2列的数为2,第1行第3列的数为6,那么第1行第100列的数为4951.
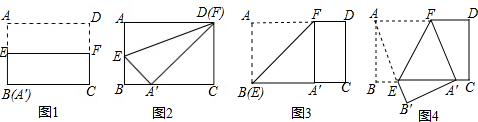
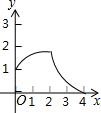
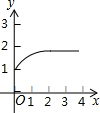
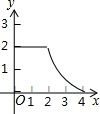
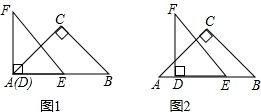 如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
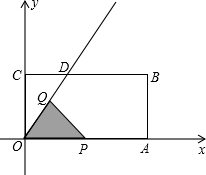 如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.
如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.