题目内容
16.在平面直角坐标系xOy中,对于任意三点A、B、C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2),B(-3,1),C(2,-2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)已知点A(1,2),B(-3,1),P(0,t).
①若A、B、P三点的“矩面积”为12,求点P的坐标;
②A、B、P三点的“矩面积”的最小值为4.
(2)已知点E(4,0),F(0,2)M(m,4m),其中m>0.若E、F、M三点的“矩面积”的为8,求m的取值范围.
分析 (1)①首先由题意可得:a=4,然后分别从:当t>2时,h=t-1,当t<1时,h=2-t,去分析求解即可求得答案;
②首先根据题意得:h的最小值为:1,继而求得A,B,P三点的“矩面积”的最小值.
(2)由E,F,M三点的“矩面积”的最小值为8,可得a=4,h=2,即可得$\left\{\begin{array}{l}{0≤m≤4}\\{0≤4m≤2}\end{array}\right.$.继而求得m的取值范围.
解答 解:(1)①由题意:a=4.
当t>2时,h=t-1,
则4(t-1)=12,可得t=4,故点P的坐标为(0,4);
当t<1时,h=2-t,
则4(2-t)=12,可得t=-1,故点P 的坐标为(0,-1);
②∵根据题意得:h的最小值为:1,
∴A,B,P三点的“矩面积”的最小值为4;
故答案为:4;
(2)∵E,F,M三点的“矩面积”为8,
∴a=4,h=2,
∴$\left\{\begin{array}{l}{0≤m≤4}\\{0≤4m≤2}\end{array}\right.$.
∴0≤m≤$\frac{1}{2}$.
∵m>0,
∴0<m≤$\frac{1}{2}$.
点评 此题考查了反比例函数的性质以及不等式组的解法.此题属于新定义题,难度较大,解题的关键是理解a与h的含义,注意掌握分类讨论思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
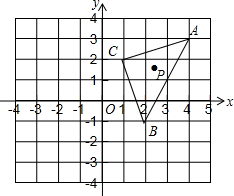 在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).
在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).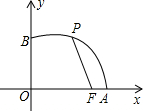 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( ) 如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.
如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.