题目内容
13．计算：（1）（-2）2+（$\sqrt{3}$-π）0+|1-2sin60°|；
（2）（x-2）2-（x+1）（x-1）．
分析 （1）原式第一项利用乘方的意义化简，第二项利用零指数幂法则计算，第三项利用绝对值的代数意义化简，计算即可得到结果；
（2）原式利用完全平方公式及平方差公式化简，计算即可得到结果．
解答 解：（1）原式=4+1+$\sqrt{3}$-1=$\sqrt{3}$+4；
（2）原式=x2-4x+4-x2+1=-4x+5．
点评 此题考查了整式的混合运算，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，点D、E分别在△ABC的边上AB、AC上，且∠ADC=∠ACB，若DE=4，AC=7，BC=8，AB=10，则AE的长为5．
4．
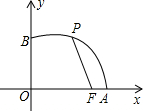如图，已知点F的坐标为（3，0），点A、B分别是某函数图象与x轴、y轴的交点，点P是此图象上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5-$\frac{3}{5}$x（0≤x≤5），则结论：①AF=2；②BF=4；③OA=5；④OB=3，正确结论的序号是（ ）
如图，已知点F的坐标为（3，0），点A、B分别是某函数图象与x轴、y轴的交点，点P是此图象上的一动点，设点P的横坐标为x，PF的长为d，且d与x之间满足关系：d=5-$\frac{3}{5}$x（0≤x≤5），则结论：①AF=2；②BF=4；③OA=5；④OB=3，正确结论的序号是（ ）| A． | ①②③ | B． | ①③ | C． | ①②④ | D． | ③④ |
2．下列各式：①${a^3}•{a^{-5}}=\frac{1}{a^2}$；②a3•a2=a6；③$\sqrt{{{（-5）}^2}}$=-5；④${（\frac{1}{3}）^{-1}}$=3；⑤（π-3.1415）0=0，其中正确的是（ ）
| A． | ①④ | B． | ③④ | C． | ②③ | D． | ④⑤ |
3．下列方程组是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{2x+3y=4}\\{2x+3=4（z+1）}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{10}{x}+3y=17}\\{8x-3y=1}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{\frac{m}{2}=1}\\{2m+n=16}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{\frac{x+2y}{z}=1}\\{\frac{2x-y}{3}=1}\end{array}\right.$ |