题目内容
9.矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A对应点A′落在线段BC上,再打开得到折痕EF.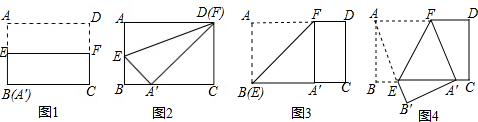
(1)当A′与B重合时(如图1),EF=5;当折痕EF过点D时(如图2),求线段EF的长?
(2)观察图3和图4,
①利用图4,证明四边形AEA′F是菱形;
②设BA′=x,当x的取值范围是3≤x≤5时,四边形AEA′F是菱形.
分析 (1)由于矩形对折,于是EF=AD=5;根据折叠的性质得到DC=AB=3,A′F=AD=5,在Rt△A′CF中利用勾股定理可计算出A′C=4,设AE=t,则BE=3-t,EA′=t,在Rt△EBA′中,利用勾股定理得(3-t)2+12=t2,解得t=$\frac{5}{3}$,然后在Rt△AEF中,利用勾股定理即可计算出EF;
(2)①根据折叠的性质得到EA=EA′,FA=FA′,∠AEF=∠A′EF,根据平行线的性质可得∠A′EF=∠AFE,则有∠A′FE=∠A′EF,于是A′E=A′F,易得AE=EA′=A′F=FA,根据菱形的判定即可得到结论.
②当折痕FE过B点时,四边形AEA′F是正方形,BA′最小,此时BA′=BA=3;当点A的对应点A′落在C点时,BA′=5,于是得到x的取值范围是3≤x≤5,四边形AEA′F是菱形;
解答 解:(1)当A′与B重合时,如图1,把矩形对折,所以EF=AD=5.
故答案为:5;
如图2,DC=AB=3,A′F=AD=5,
在Rt△A′CF中,A′C=$\sqrt{A′{F}^{2}-F{C}^{2}}$=4,
设AE=t,则BE=3-t,EA′=t,
在Rt△EBA′中,BA′=BC-A′C=5-4=1,
∵BE2+BA′2=EA′2,
∴(3-t)2+12=t2,解得t=$\frac{5}{3}$,
在Rt△AEF中,AE=$\frac{5}{3}$,AF=5,
∴EF=$\sqrt{(\frac{5}{3})^{2}+{5}^{2}}$=$\frac{5\sqrt{10}}{3}$;
(2)①如图4,∵△AEF沿EF折叠到△A′EF,
∴EA=EA′,FA=FA′,∠AEF=∠A′EF,
∵四边形ABCD为矩形,
∴AF∥EC,
∴∠A′EF=∠AFE,
∴∠A′FE=∠A′EF,
∴A′E=A′F,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形.
②当折痕FE过B点时,四边形AEA′F是正方形,BA′最小,此时BA′=BA=3;当点A的对应点A′落在C点时,BA′=5,于是得到x的取值范围是3≤x≤5,四边形AEA′F是菱形,
故答案为:3≤x≤5;
点评 本题考查了折叠的性质:折叠前后两图形全等,折痕垂直平分对应点的连线段.也考查了矩形的性质、勾股定理以及菱形的判定与性质.

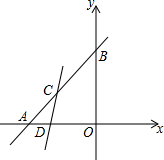
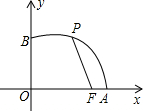 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )| A. | ①②③ | B. | ①③ | C. | ①②④ | D. | ③④ |
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | A | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | B | 1 |
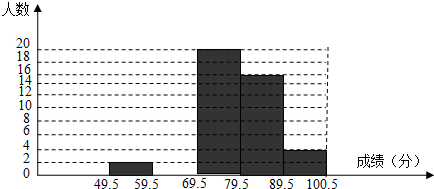
(1)频数、频率分布表中a=8,b=0.08;(答案直接填在题中横线上 )
(2)补全频数分布直方图;
(3)若该校八年级共有600名学生,且各个班级学生成绩分布基本相同,请估计该校八年级上学期期末考试成绩低于70分的学生人数.
 如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1
如图,S△AOB=18,且△AOB为等腰直角三角形,C为AB中点,过点C的直线l把△AOB面积分成5:1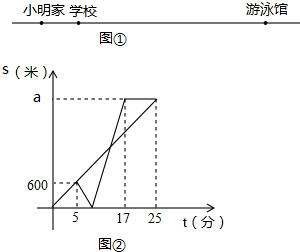 图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.
图①是小明家、学校和游泳馆之间的位置关系示意图,某天放学后,小亮和小明同时从学校出发,小亮匀速步行前往游泳馆,小明先匀速步行回家取游泳用品,然后骑自行车原路返回,沿与小亮相同的路线前往游泳馆,小明骑自行车的速度始终不变,小亮和小明各自与学校的距离s(米)与所用时间t(分)之间的函数图象的如图②所示.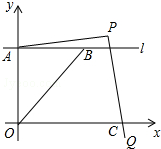 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.