题目内容
7.化简:(1)(a+2)(a-3)-(2-a)2
(2)$\frac{{{{({x+2})}^2}}}{{{x^2}-4}}+\frac{x+1}{x-2}-({2-\frac{2x}{x+1}})$.
分析 (1)根据多项式乘以多项式以及完全平方公式进行计算即可;
(2)先通分,再分解因式,然后约分计算即可.
解答 解:(1)原式=a2-a-6-4+4a-a2
=3a-10;
(2)原式=$\frac{(x+2)^{2}}{(x+2)(x-2)}$+$\frac{x+1}{x-2}$-$\frac{2x+2-2x}{x+1}$
=$\frac{x+2}{x-2}$+$\frac{x+1}{x-2}$-$\frac{2}{x+1}$
=$\frac{(2x+3)(x+1)}{(x-2)(x+1)}$-$\frac{2(x-2)}{(x-2)(x+1)}$
=$\frac{2{x}^{2}+5x+3-2x+4}{(x-2)(x+1)}$
=$\frac{2{x}^{2}+3x+7}{{x}^{2}-x-2}$.
点评 本题考查了整式的混合运算、分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
15.下列关于x的方程中,一定是一元二次方程的是( )
| A. | x-2=0 | B. | x2-4x-1=0 | C. | 3x2+$\frac{2}{x}$-4=0 | D. | xy+1=0 |
 如图,已知∠AOB=60°,点P在边OA上,OP=16,点M,N在边OB上,PM=PN,若MN=4,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=16,点M,N在边OB上,PM=PN,若MN=4,则OM=( ) 如图,△ABC≌△DBC,∠A=110°,则∠D=110°.
如图,△ABC≌△DBC,∠A=110°,则∠D=110°.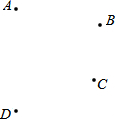 如图,已知平面上有四点A、B、C、D,按要求作图
如图,已知平面上有四点A、B、C、D,按要求作图 过线段AB上的一点P作线段AB的垂线.(保留作图痕迹,不写作法)
过线段AB上的一点P作线段AB的垂线.(保留作图痕迹,不写作法)