题目内容
5.若一次函数y=(a+3)x+a-3不经过第二象限,则a的取值范围是-3<a≤3.分析 先判断一次函数y=(a+3)x+a-3经过第一、三、四象限或过原点,再根据一次函数与系数的关系得到a+3>0且a-3≤0,然后求出两个不等式的公共部分即可.
解答 解:∵一次函数y=(a+3)x+a-3不经过第二象限,
即一次函数y=(a+3)x+a-3经过第一、三、四象限或过原点,
∴a+3>0且a-3≤0,
∴a的取值范围是-3<a≤3.
故答案为-3<a≤3.
点评 本题考查了一次函数与系数的关系:对于一次函数y=kx+b,它与y轴交于(0,b),当b>0时,(0,b)在y轴的正半轴上,直线与y轴交于正半轴;当b<0时,(0,b)在y轴的负半轴,直线与y轴交于负半轴.当k>0,b>0?y=kx+b的图象在一、二、三象限;k>0,b<0?y=kx+b的图象在一、三、四象限;k<0,b>0?y=kx+b的图象在一、二、四象限;k<0,b<0?y=kx+b的图象在二、三、四象限.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
15.下列计算正确的是( )
| A. | x2+3x2=4x4 | B. | x2y•2x3=2x6y | C. | (6x3y2)÷(3x)=2x2 | D. | (-3x)2=9x2 |
13.解关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$时会产生增根,则增根可能为( )
| A. | 0或3 | B. | 3 | C. | 0 | D. | 以上都不对 |
20.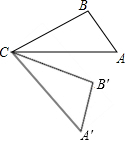 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |