题目内容
20.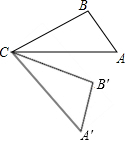 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,若∠A=40°,∠B′=110°,则∠A′CB的度数是( )| A. | 110° | B. | 80° | C. | 40° | D. | 30° |
分析 首先根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,即可得到∠A′=40°,再有∠B′=110°,利用三角形内角和可得∠A′CB′的度数,进而得到∠ACB的度数,再由条件将△ABC绕着点C顺时针旋转50°后得到△A′B′C′可得∠ACA′=50°,即可得到∠BCA′的度数.
解答 解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°-110°-40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°.
故选:B.
点评 此题主要考查了旋转的性质,关键是熟练掌握旋转前、后的图形全等,进而可得到一些对应角相等.

练习册系列答案
相关题目
8.下列计算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | B. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | C. | $\sqrt{12}$÷$\sqrt{3}$=2 | D. | $\sqrt{12}$=2$\sqrt{3}$ |
10.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
| A. | 当∠A=60°时,它是菱形 | B. | 当AC⊥BD时,它是菱形 | ||
| C. | 当AC=BD时,它是矩形 | D. | 当AB=BC,AC=BD时,它是正方形 |
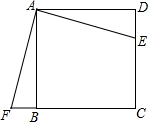 如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形.
如图,四边形ABCD是正方形,△ABF和△ADE经旋转后得到的,则可知旋转中心为点A,旋转了90度,如果连接EF,那么△AEF是等腰直角三角形. 如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于4$\sqrt{13}$.
如图,矩形ABCD的长和宽分别为6和4,E、F、G、H依次是矩形ABCD各边的中点,则四边形EFGH的周长等于4$\sqrt{13}$.