题目内容
14．若a、b为正整数．且a＞$\sqrt{10}$，b＜$\sqrt{6}$，则a+b的最小值为5．分析 先估算出a、b的取值范围，然后再求得a+b的最大值即可．
解答 解：∵9＜10＜16，4＜6＜9，
∴3＜$\sqrt{10}$＜4，2＜$\sqrt{6}$＜3．
又∵a、b为正整数，
∴当a=4，b=1时，a+b有最小值，
∴a+b的最小值为5．
故答案为：5．
点评 本题主要考查的是估算无理数的大小，熟练掌握估算无理数大小的方法是解题的关键．
练习册系列答案
相关题目
4．若关于x的不等式组$\left\{\begin{array}{l}{x-a＞0}\\{1-2x＞x-2}\end{array}\right.$的解集中只有4个整数解，则a取值范围是-4≤a＜-3．
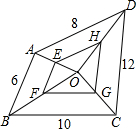如图，点O为四边形ABCD内任意一点，E，F，G，H分别为边OA，OB，OC，OD的中点，则四边形EFGH的周长=18．
4．已知a＜b，则下列不等式一定成立的是（ ）
| A． | a2＜ab | B． | ab＜b2 | C． | $\frac{3}{2}a＞\frac{3}{2}b$ | D． | 7a-7b＜0 |