题目内容
10.先化简,再求值:($\frac{1}{a-b}$-$\frac{1}{a+b}$)÷$\frac{b}{{a}^{2}+2ab{+b}^{2}}$,其中a=1+$\sqrt{2}$,b=1-$\sqrt{2}$.分析 先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可.
解答 解:原式=$\frac{a+b-a+b}{(a-b)(a+b)}$•$\frac{(a+b)^{2}}{b}$
=$\frac{2b}{(a-b)(a+b)}$•$\frac{{(a+b)}^{2}}{b}$
=$\frac{2(a+b)}{a-b}$,
当a=1+$\sqrt{2}$,b=1-$\sqrt{2}$时,原式=$\frac{2(1+\sqrt{2}+1-\sqrt{2})}{1+\sqrt{2}-1+\sqrt{2}}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
20.设4-$\sqrt{2}$的整数部分为a,小数部分为b,则a-$\frac{1}{b-2}$的值为( )
| A. | 2+$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | -$\sqrt{2}$ |
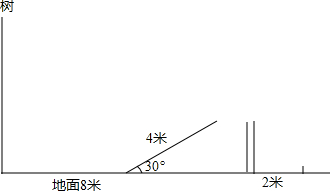 树照在地面影子长8米,照在斜坡上4米,已知斜坡角度30度,同一时刻将1米木棍竖直在地面上,影子长2米,求:树高.
树照在地面影子长8米,照在斜坡上4米,已知斜坡角度30度,同一时刻将1米木棍竖直在地面上,影子长2米,求:树高.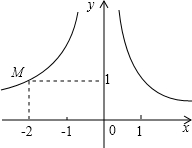 如图,已知双曲线y1=$\frac{{k}_{1}}{x}$(x>0),双曲线y2=-$\frac{{k}_{2}}{x}$(x<0)经过M点,且k2=2k1.
如图,已知双曲线y1=$\frac{{k}_{1}}{x}$(x>0),双曲线y2=-$\frac{{k}_{2}}{x}$(x<0)经过M点,且k2=2k1.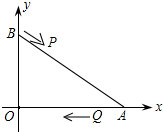 如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t秒(0<t<$\frac{10}{4}$).解答如下问题:
如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t秒(0<t<$\frac{10}{4}$).解答如下问题: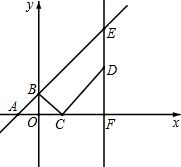 如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.
如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于点A,B.点C的坐标为(m,0),将线段BC绕点C顺时针旋转90°,并延长一倍得CD,过点D作x轴的垂线,垂足为F,交直线AB于点E.