题目内容
20.设4-$\sqrt{2}$的整数部分为a,小数部分为b,则a-$\frac{1}{b-2}$的值为( )| A. | 2+$\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | -$\sqrt{2}$ |
分析 根据1<$\sqrt{2}$<2,不等式的性质,可得a、b的值,根据代数式求值,可得答案.
解答 解:由1<$\sqrt{2}$<2,得-2<-$\sqrt{2}$<-1,
由不等式的性质,得
2<4-$\sqrt{2}$<3,
a=2,b=4-$\sqrt{2}$-2=2-$\sqrt{2}$,
当a=2,b=2-$\sqrt{2}$时,a-$\frac{1}{b-2}$=2-$\frac{1}{2-\sqrt{2}-2}$=2+$\frac{\sqrt{2}}{2}$,
故选:A.
点评 本题考查了估算无理数的大小,利用了被开方数越大算术平方根越大,还利用了不等式的性质.

练习册系列答案
相关题目
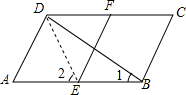 已知如图所示,在?ABCD中,∠A=60°,E,F分别是AB,CD中点,AB=2AD.求证:BD=$\sqrt{3}$EF.
已知如图所示,在?ABCD中,∠A=60°,E,F分别是AB,CD中点,AB=2AD.求证:BD=$\sqrt{3}$EF.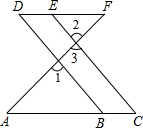 如图所示,已知在四边形BCED中,A是CB延长线上的点,连接AF,如果∠1=∠2,∠C=∠D,请说明AC∥DF.
如图所示,已知在四边形BCED中,A是CB延长线上的点,连接AF,如果∠1=∠2,∠C=∠D,请说明AC∥DF.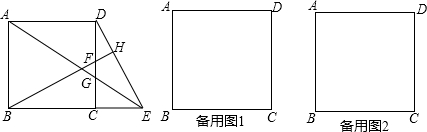
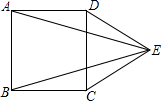 如图,以正方形ABCD的DC边为一边向外作一个等边三角形CDE.
如图,以正方形ABCD的DC边为一边向外作一个等边三角形CDE.