题目内容
1.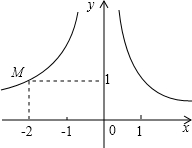 如图,已知双曲线y1=$\frac{{k}_{1}}{x}$(x>0),双曲线y2=-$\frac{{k}_{2}}{x}$(x<0)经过M点,且k2=2k1.
如图,已知双曲线y1=$\frac{{k}_{1}}{x}$(x>0),双曲线y2=-$\frac{{k}_{2}}{x}$(x<0)经过M点,且k2=2k1.(1)求双曲线y1与y2的解析式;
(2)若平行于x轴的直线l交双曲线y1于点A,交双曲线y2于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
分析 (1)把M坐标代入y2解析式求出k2的值,确定出y2解析式,根据k2=2k1,求出k1的值,确定出y1解析式;
(2)如图所示,设A(a,$\frac{1}{a}$),进而表示出B,C,D坐标,确定出CD与AD的长,表示出矩形ABCD周长,根据周长为8求出a的值,即可确定出满足题意C与D的坐标.
解答 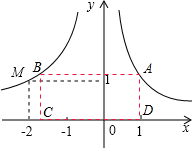 解:(1)把M(-2,1)代入y2=-$\frac{{k}_{2}}{x}$,得:k2=2,
解:(1)把M(-2,1)代入y2=-$\frac{{k}_{2}}{x}$,得:k2=2,
∴k1=1,
则y1=$\frac{1}{x}$(x>0),y2=-$\frac{2}{x}$(x<0);
(2)设A坐标为(a,$\frac{1}{a}$),a>0,可得D(a,0),即OD=a,AD=$\frac{1}{a}$,
把y=$\frac{1}{a}$代入y2=-$\frac{2}{x}$中,得:x=-2a,即B(-2a,$\frac{1}{a}$),
∴C(-2a,0),即OC=2a,
∴CD=OC+OD=2a+a=3a,
∵矩形ABCD周长为8,
∴2(CD+AD)=8,即CD+AD=4,
∴3a+$\frac{1}{a}$=4,即3a2-4a+1=0,
解得:a=$\frac{1}{3}$或a=1,
当a=$\frac{1}{3}$时,C(-$\frac{2}{3}$,0),D($\frac{1}{3}$,0);
当a=1时,C(-2,0),D(1,0),
综上,C(-$\frac{2}{3}$,0),D($\frac{1}{3}$,0)或C(-2,0),D(1,0).
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法求反比例函数解析式,矩形的性质,坐标与图形性质,熟练掌握待定系数法是解本题第一问的关键.

练习册系列答案
相关题目
11.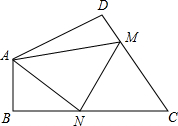 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )| A. | 90° | B. | 100° | C. | 130° | D. | 140° |
9.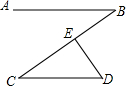 如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为( )
如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为( )
 如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为( )
如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为( )| A. | 40° | B. | 50° | C. | 38° | D. | 60° |
6.下列计算中,正确的是( )
| A. | b5+b5=b10 | B. | a3•a3=2a3 | C. | (a3)3=a6 | D. | a3÷a3=1(a≠0) |
13.下列计算正确的( )
| A. | 2$\sqrt{3}$+3$\sqrt{3}$=5$\sqrt{6}$ | B. | ($\sqrt{2}$+1)(1-$\sqrt{2}$)=1 | C. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ | D. | -(-a)4÷a2=a2 |