题目内容
12．已知点（2，y1），（-3，y2）均在抛物线y=x2-1上，则y1、y2的大小关系为（ ）| A． | y1＜y2 | B． | y1＞y2 | C． | y1≤y2 | D． | y1≥y2 |
分析 先根据二次函数的性质得到抛物线的对称轴为直线x=0，然后比较两个点离直线x=0的远近得到y1、y2的大小关系．
解答 解：∵二次函数的解析式为y=x2-1，
∴抛物线的对称轴为直线x=0，
∵（2，y1）、B（-3，y2），
∴点（-3，y2）离直线x=0远，点（2，y1）离直线x=0近，
而抛物线开口向上，
∴y1＜y2．
故选A．
点评 本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
阅读快车系列答案
相关题目
2．满足等式（x+3）${\;}^{-{x}^{2}+x+2}$=1的所有实数x的和是（ ）
| A． | 1 | B． | -1 | C． | -5 | D． | -6 |
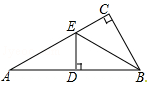如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE+DE等于3cm．