题目内容
2.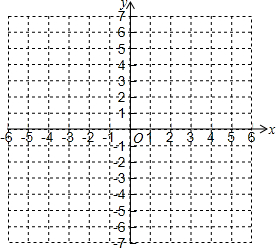 在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2);
在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2); (1)顺次连接A,B,C,组成△ABC,求△ABC的面积.
(2)如果△A′B′C′与△ABC关于直线y=-1对称,画出△A′B′C′,并写出A′﹑B′﹑C′三点的坐标.
分析 (1)根据图形平移的性质描出B点,顺次连接A,B,C,利用矩形的面积减去三个顶点上三角形的面积即可;
(2)作出直线y=-1,根据轴对称的性质作出△A′B′C′,并写出A′﹑B′﹑C′三点的坐标即可.
解答  解:(1)如图所示,S△ABC=4×5-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×5
解:(1)如图所示,S△ABC=4×5-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×2×5
=20-3-4-5
=8;
(2)如图所示,由图可知,A′(-1,-2),B′(1,-6),C′(4,-4).
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
相关题目
12.下列多项式乘法中,能用平方差公式计算的是( )
| A. | (a+b2)(a2-b) | B. | (a+2)(2+a) | C. | (-a+b)(a-b) | D. | (2a+b)(-2a+b) |
13.方程3-2(x-5)=9的解是( )
| A. | x=-2 | B. | x=2 | C. | x=$\frac{2}{3}$ | D. | x=1 |
14.和-2的相反数相等的是( )
| A. | -2的平方 | B. | -2的倒数 | C. | -2的绝对值 | D. | 4的平方根 |
 如图所示,矩形ABCD沿EF折叠,若∠DEF=72°,则∠AEG的度数为36°.
如图所示,矩形ABCD沿EF折叠,若∠DEF=72°,则∠AEG的度数为36°.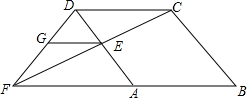 如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.
如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.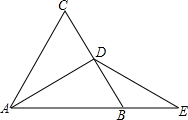 如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.
如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.