题目内容
7.计算:($\sqrt{xy}$-$\frac{xy}{x+\sqrt{xy}}$)÷$\frac{\sqrt{xy}-y}{x-y}$.分析 首先将括号里面分母有理化,再通分运算,结合二次根式除法运算法则化简求出即可.
解答 解:($\sqrt{xy}$-$\frac{xy}{x+\sqrt{xy}}$)÷$\frac{\sqrt{xy}-y}{x-y}$
=[$\sqrt{xy}$-$\frac{xy(x-\sqrt{xy})}{(x+\sqrt{xy})(x-\sqrt{xy})}$]×$\frac{x-y}{\sqrt{xy}-y}$
=[$\sqrt{xy}$-$\frac{y(x-\sqrt{xy})}{x-y}$]×$\frac{x-y}{\sqrt{xy}-y}$
=$\frac{(x-y)\sqrt{xy}-y(x-\sqrt{xy})}{x-y}$×$\frac{x-y}{\sqrt{xy}-y}$
=$\frac{x(\sqrt{xy}-y)}{x-y}$×$\frac{x-y}{\sqrt{xy}-y}$
=x.
点评 此题主要考查了二次根式的混合运算,正确分母有理化是解题关键.

练习册系列答案
相关题目
18.下列命题中,真命题是( )
| A. | 对角线互相垂直且平分的四边形是正方形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 四个角相等的四边形是矩形 | |
| D. | 一组对边平行另一组对边相等的四边是平行四边形 |
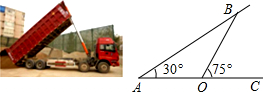 如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2$\sqrt{3}$+2)米.试求货车卸货时举升杠杆OB的长.
如图是某种自动卸货时的示意图,AC时水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC夹角为30°,举升杠杆OB与底盘AC夹角为75°,已知举升杠杆上顶点B离火车支撑点A的距离为(2$\sqrt{3}$+2)米.试求货车卸货时举升杠杆OB的长.