题目内容

18．求不等式组$\left\{\begin{array}{l}{5x-1＜3x+1}\\{\frac{x+1}{3}≤\frac{3x+1}{2}+1}\end{array}\right.$的整数解．

分析 首先解每个不等式，两个不等式的解集的公共部分就是解集的公共部分，然后确定整数解即可．

解答 解：$\left\{\begin{array}{l}{5x-1＜3x+1…①}\\{\frac{x+1}{3}≤\frac{3x+1}{2}+1…②}\end{array}\right.$，
解①得：x＜1，
解②得：x≥-1，
则不等式组的解集是：-1≤x＜1，则整数解是-1，0．

点评 本题考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．

练习册系列答案
相关题目
8．一次函数y=-3x+6的图象不经过（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
9．在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，甲、乙参加表演的8个女演员身高的方差分别为S甲2=1.5，S乙2=2.5，则甲芭蕾舞团的身高更整齐（填“甲”或“乙”）．
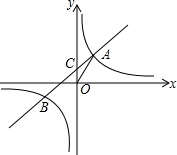6．定义：一次函数y=ax+b的特征数为[a，b]，反比例函数y=$\frac{k}{x}$的特征数为[1，k]．
（1）若特征数是[1，p-1]的一次函数为正比例函数，求p的值；
（2）如图，若一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象分别交于第一、第三象限的A、B两点，与y轴正半轴交于点C，点A的坐标为（m，2），点B的坐标为（-2，n），tan∠AOC=$\frac{1}{2}$．求该一次函数和反比例函数的特征数．
13．计算：$\root{3}{-8}$-$\sqrt{2}$+（$\sqrt{3}$）2+|1-$\sqrt{2}$|．
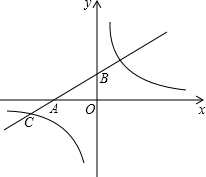3．如图，在平面直角坐标系中，直线y=ax+1（a≠0）与x轴交于点A，与y轴交于点B，与双曲线y=$\frac{k}{x}$在第三象限的交点为C（-2$\sqrt{3}$，m），且△AOC的面积为$\frac{{\sqrt{3}}}{2}$．
（1）求a的值；
（2）求m、k的值；
（3）以BC为一边作等边△BCD，求点D的坐标．
10．菱形的两条对角线长分别为18与24，则此菱形的周长为（　　）
A．15B．30C．60D．120
7．计算：（$\sqrt{xy}$-$\frac{xy}{x+\sqrt{xy}}$）÷$\frac{\sqrt{xy}-y}{x-y}$．
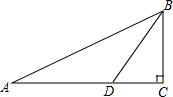8．如图，在△ABC中，∠C=90°，点D在边AC上，且∠DBC=∠A，若AC=25，tanA=$\frac{2}{5}$．
（1）BC的长；
（2）∠BDC的余弦值；
（3）AD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网