题目内容
4.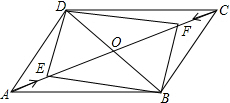 如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
分析 设经过t秒后,四边形BPDE是矩形;由平行四边形的性质得出OA=OC=$\frac{1}{2}$AC=6,OB=OD=$\frac{1}{2}$BD=4,得出OE=OF,证出四边形BFDE是平行四边形,当EF=BD,即OE=OD时,四边形BFDE是矩形,得出6-t=4,或t-6=2,解方程即可.
解答 解:设经过t秒后,四边形BPDQ是矩形;
则AE=CF=t,
∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC=6,OB=OD=$\frac{1}{2}$BD=4,
∴OE=OF,
∴四边形BFDE是平行四边形,
当EF=BD,即OE=OD时,四边形BFDE是矩形,
此时6-t=4,或t-6=2,
解得:t=2,或t=8,
即经过2秒或8秒后,四边形BPDE是矩形.
点评 本题考查了矩形的判定、平行四边形的性质与判定;熟练掌握平行四边形的性质与判定,由对角线相等得出方程是解决问题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
12.下列各式计算正确的是( )
| A. | 3a+2b=5 | B. | a5÷a=a4 | C. | (-2a2)3=-6a6 | D. | 3a-2=$\frac{1}{9{a}^{2}}$ |
14.在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,a+c=2b且c-a=$\frac{1}{2}$b,△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
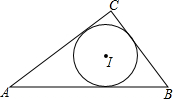 如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$.
如图,△ABC中,已知AB=8,BC=5,AC=7,则它的内切圆的半径为$\sqrt{3}$. 已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.
已知△ABC中,AC=6cm,BC=8cm,AB=10cm,CD为AB边上的高.动点P从点A出发,沿着△ABC的三条边逆时针走一圈回到A点,速度为2cm/s,设运动时间为ts.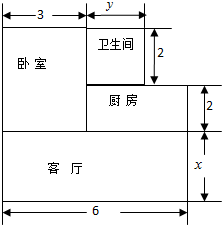 小王家购买了一套经济适用房,他家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
小王家购买了一套经济适用房,他家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题: