题目内容
19.在平面直角坐标系xOy中,已知两点A(-1,0),B(-2,3),在y轴上求作一点P,使AP+BP最短,并求出点P的坐标.分析 作出A点关于y轴的对称点D,连接BD,交y轴于P,此时AC+BC最短;根据B、D的坐标利用待定系数法求一次函数解析式进而得出P点坐标.
解答  解:作出A点关于y轴的对称点D,连接BD,交y轴于P,此时AC+BC最短;
解:作出A点关于y轴的对称点D,连接BD,交y轴于P,此时AC+BC最短;
设BD所在直线解析式为:y=kx+b,
∵A(-1,0),
∴D(1,0),
将B(-2,3),D(2,0)代入得:
$\left\{\begin{array}{l}{-2k+b=3}\\{k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
∴直线BD的解析式为:y=-x+1,
当x=0时,y=1,
∴P点坐标为:(0,1).
点评 此题主要考查了关于坐标轴对称点的性质以及待定系数法求一次函数解析式等知识,利用已知得出直线BD解析式是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
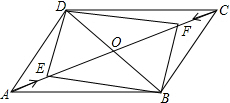 如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?
如图,在平行四边形ABCD中,角线AC、BD相交于点O,动点E以1个单位每秒的速度从点A出发沿AC向运动,点F同时以1个单位每秒的速度从点C发沿CA方向运动,若AC=12,BD=8,求出经过几秒后,四边形BPDQ是矩形?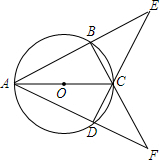 如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°.
如图,四边形ABCD内接于⊙O,AB与DC的延长线交于点E,AD与BC的延长线交于点F.若∠E=∠F=44°. 在平面直角坐标系中,△ABC的位置如图所示,△DEF的顶点坐标分别为D(0,-1)、E(-4,-3)、F(-1.-3).
在平面直角坐标系中,△ABC的位置如图所示,△DEF的顶点坐标分别为D(0,-1)、E(-4,-3)、F(-1.-3).