Question

10．如图所示，抛物线过点O（0，0），A（3，3），B（4，0）．
（1）求此抛物线的解析式；
（2）M为直线OA上方抛物线上的一个动点．求四边形OMAB的最大面积．

Answer 1

分析 （1）设抛物线解析式为y=ax²+bx+c，把点O、A、B的坐标代入求解即可；
（2）设出M点的坐标，再把四边形OMAB的面积分成两个直角三角形与一个梯形的面积列式进行整理，利用二次函数的性质探讨得出答案即可．

解答 解：（1）设抛物线解析式为y=ax²+bx+c，
∵抛物线过点O（0，0），A（3，3）和B（4，0），
∴$\left\{\begin{array}{l}{c=0}\\{9a+3b+c=3}\\{16a+4b+c=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=0}\end{array}\right.$，
所以，抛物线的解析式为y=-x²+4x；

（2）如图，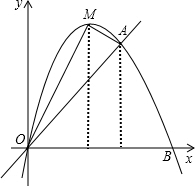

设M坐标为（x，-x²+4x），
四边形OMAB的面积=$\frac{1}{2}$x（-x²+4x）+$\frac{1}{2}$（3-x²+4x）（3-x）+$\frac{1}{2}$×（4-3）×3
=-$\frac{3}{2}$x²+$\frac{9}{2}$x+6
=-$\frac{3}{2}$（x-$\frac{3}{2}$）²+$\frac{75}{8}$，
因此四边形OMAB的最大面积是$\frac{75}{8}$．

点评 本题考查了待定系数法求二次函数解析式，是求函数解析式常用的方法，一定要熟练掌握，把不规则四边形的面积分成常见的图形求面积是常用的方法．