题目内容
2.计算:(1)$\frac{\sqrt{50}×\sqrt{32}}{\sqrt{8}}$-4;
(2)$\frac{\sqrt{24}×\sqrt{216}}{\sqrt{6}}$+5;
(3)($\sqrt{6}$-2$\sqrt{15}$)×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$;
(4)$\sqrt{\frac{2}{3}}$-4$\sqrt{216}$+42$\sqrt{\frac{1}{6}}$.
分析 (1)首先化简二次根式进而求出即可;
(2)首先化简二次根式进而求出即可;
(3)直接利用二次根式乘法运算法则化简,进而合并求出即可;
(4)直接化简二次根式进而合并同类二次根式即可.
解答 解:(1)$\frac{\sqrt{50}×\sqrt{32}}{\sqrt{8}}$-4
=5$\sqrt{2}$×2-4
=10$\sqrt{2}$-4;
(2)$\frac{\sqrt{24}×\sqrt{216}}{\sqrt{6}}$+5
=2×6$\sqrt{6}$+5
=12$\sqrt{6}$+5;
(3)($\sqrt{6}$-2$\sqrt{15}$)×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$
=3$\sqrt{2}$-6$\sqrt{5}$-6×$\frac{\sqrt{2}}{2}$
=-6$\sqrt{5}$;
(4)$\sqrt{\frac{2}{3}}$-4$\sqrt{216}$+42$\sqrt{\frac{1}{6}}$
=$\frac{\sqrt{6}}{3}$-4×6$\sqrt{6}$+7$\sqrt{6}$
=-$\frac{50}{3}$$\sqrt{6}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
 如图所示,抛物线过点O(0,0),A(3,3),B(4,0).
如图所示,抛物线过点O(0,0),A(3,3),B(4,0). 如图,AF∥CD,AB⊥BC,∠A=122°.
如图,AF∥CD,AB⊥BC,∠A=122°.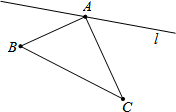 如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?
如图,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?