题目内容
17.x为何值时,分式$\frac{1}{2x-1}$与$\frac{2}{3x+2}$的值相等?并求出此时分式的值.分析 先列出方程$\frac{1}{2x-1}$=$\frac{2}{3x+2}$,再求解即可.
解答 解:∵分式$\frac{1}{2x-1}$与$\frac{2}{3x+2}$的值相等,
∴$\frac{1}{2x-1}$=$\frac{2}{3x+2}$,
∴3x+2=4x-2,
解得x=4,
检验:把x=4代入(2x-1)(3x+2)=7×14=98≠0,
∴x=4是原方程的解,
把x=4代入$\frac{1}{2x-1}$,得$\frac{1}{2×4-1}$=$\frac{1}{7}$,
∴x=4时,分式的值为$\frac{1}{7}$.
点评 本题考查了解分式方程,注意:
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.

练习册系列答案
相关题目
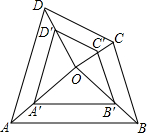 如图,点O是四边形ABCD与A′B′C′D′的位似中心,3OA′=2OA,则$\frac{A'B'}{AB}$=$\frac{2}{3}$.
如图,点O是四边形ABCD与A′B′C′D′的位似中心,3OA′=2OA,则$\frac{A'B'}{AB}$=$\frac{2}{3}$. 已知AD∥CB,AE、BE分别平分∠DAC和∠ABC,若∠E=∠BAC,则∠E=60°.
已知AD∥CB,AE、BE分别平分∠DAC和∠ABC,若∠E=∠BAC,则∠E=60°.