题目内容
1．
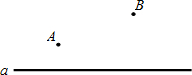如图，直线a表示一条公路，点A、B表示两个乡镇．如果要在公路旁（直线a上）修一个车站S，使得AS+BS最小，请作出点S．
分析 画出点A关于直线a的对称点A′，连接A′B交a于点S，连接AS，由对称的性质可知AS=A′S，由两点之间线段最短可知点S即为所求点．
解答 解：画出点A关于直线a的对称点A′，连接A′B交a于点S，连接AS，
∵A、A′关于直线a对称，
∴AS=A′S，
∴AS+BS=A′B，
由两点之间线段最短可知，线段A′B的长即为AS+BS的最小值，故S点即为所求点．
．
点评 本题考查的是最短线路问题，熟知对称的性质及两点之间线段最短的知识是解答此题的关键．
练习册系列答案
相关题目
敌军基地在三条公路围成的三角区域内，我军一队战士在一条公路中点垂直射击，另一队战士在另一条公路中点垂直射击，均击中敌军基地，问第三队战士在公路何处垂直射击可击中目标？
如图，EF∥CD，EF∥AB，求证：EM=FN．
6．在下列条件中不能判定△ABC∽△DEF的是（ ）
| A． | ∠D=40°，∠E=80°，∠A=60°，∠B=80° | |
| B． | ∠A=∠D，AB：AC=DF：EF | |
| C． | ∠B=∠E=90°，BC：EF=AC：DF | |
| D． | AB=1，BC=2，CA=1.5，DE=6，EF=4，FD=8 |
有一块长为30m，宽为20m的矩形菜地，准备修筑同样宽的三条直路（如图），把菜地分成六块作为试验田，种植不同品种的蔬菜，并且种植蔬菜面积为矩形菜地面积的$\frac{3}{4}$，设道路的宽度为x m，下列方程：