题目内容
11.某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出300件;若按每件6元的价格销售,每月能卖出200件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.(1)试求y与x之间的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
分析 (1)设出解析式,把(5,300),(6,200)代入求出系数即可;
(2)根据题意列出二次函数解析式,根据二次函数的性质求出最值即可.
解答 解:(1)由题意,可设y=kx+b,把(5,300),(6,200)代入得:
$\left\{\begin{array}{l}300=5k+b\\ 200=6k+b\end{array}\right.$,解得:$\left\{\begin{array}{l}k=-100\\ b=800\end{array}\right.$,
所以y与x之间的关系式为:y=-100x+800;
(2)设利润为W,则W=(x-4)(-100x+800)
=-100 (x-4)(x-8)
=-100 (x2-12x+32)
=-100[(x-6)2-4]
=-100 (x-6)2+400
所以当x=6时,W取得最大值,最大值为400元.
答:当销售价格定为6元时,每月的利润最大,每月的最大利润为400元.
点评 本题考查的是待定系数法求一次函数解析式和二次函数的应用,正确运用待定系数法、掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
3.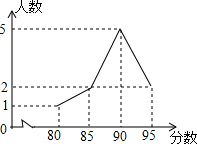 在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
 在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的学校跳操比赛中,九年级参赛的10名学生成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
20.若$\sqrt{x-1}$+(y+1)2=0,则x-y的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
 如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形.
如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形. 如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°.
如图,直线a∥b,点B在直线b上,∠1=38°,∠ABC=90°,则∠2=52°. 如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.
如图中所示是一圆锥形的零件经过轴的剖面,它的腰长等于圆锥的母线长,底边长等于圆锥底面的直径,按图中表明的尺寸求这个零件的母线长为36.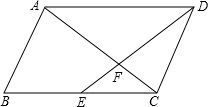 点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.
点E是平行四边形ABCD边BC的中点,平行四边形ABCD的面积是m,则四边形ABEF的面积是$\frac{5}{12}$m.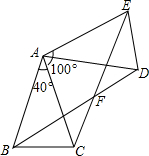 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.