题目内容
2. 如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形.
如图,第①个图形中一共有1个矩形,第②个图形中一共有5个矩形,第③个图形中一共有11个矩形,…则第n个图形中一共有n2+n-1矩形.
分析 由图②矩形有5个=(2+2)(2-1)+1,图③矩形有11个=(2+3)(3-1)+1,图④矩形有19=(2+4)(4-1)+1,…由此得出第n个图形矩形的个数是(2+n)(n-1)+1.
解答 解:∵图②矩形有5个=$\frac{2×(2+1)}{2}$×2-1,
图③矩形有11个=$\frac{3×(3+1)}{2}$×2-1,
…
∴第n个图有$\frac{n(n-1)}{2}$×2-1=n2+n-1个矩形.
故答案为:n2+n-1.
点评 此题考查图形的变化规律,根据图形进行数字猜想的问题,关键是通过归纳与总结,得到其中的规律,然后利用规律解决一般问题.

练习册系列答案
相关题目
19.要使代数式$\frac{1}{\sqrt{3x-1}}$有意义,则x的取值范围是( )
| A. | x>$\frac{1}{3}$ | B. | x<-$\frac{1}{3}$ | C. | x<$\frac{1}{3}$ | D. | x>-$\frac{1}{3}$ |
7.将正奇数按下表排成5列:
第一列第二列第三列第四列第五列
第一行 1 3 5 7
第二行 15 13 11 9
第三行 17 19 21 23
第四行 31 29 27 25
…
根据上面规律,2007应在( )
第一列第二列第三列第四列第五列
第一行 1 3 5 7
第二行 15 13 11 9
第三行 17 19 21 23
第四行 31 29 27 25
…
根据上面规律,2007应在( )
| A. | 125行,3列 | B. | 125行,2列 | C. | 251行,2列 | D. | 251行,5列 |
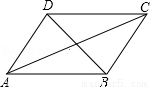

 已知:如图,?ABCD中,∠BCD的平分线交AB于点E,交侧的延长线于点F.
已知:如图,?ABCD中,∠BCD的平分线交AB于点E,交侧的延长线于点F.