题目内容
4.观察下列化简过程:①$\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{6}}{3}$
②$\frac{1}{\sqrt{18}}$=$\frac{1}{3\sqrt{2}}$=$\frac{1×\sqrt{2}}{3\sqrt{2}×\sqrt{2}}$=$\frac{\sqrt{2}}{6}$
③$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1
以上过程都是通过恒等值变形,将分母的根号(或根号中的分母)去掉,我们把这个过程叫做分母有理化,变形中分子分母分别乘的式子叫做它们的有理化因式,如①中的有理化因式是$\sqrt{3}$,②中的有理化因式是$\sqrt{2}$,③中的有理化因式是$\sqrt{2}$-1,解答下列问题:
(1)二次根式$\frac{1}{\sqrt{27}}$、$\sqrt{\frac{3}{8}}$、$\frac{3}{\sqrt{7}-2}$的有理化因式分别为$\sqrt{3}、\sqrt{2}、\sqrt{7}+2$;
(2)第(1)题中二次根式化简的结果分别为$\frac{\sqrt{3}}{9}、\frac{\sqrt{6}}{4}、\sqrt{7}+2$;
(3)计算:($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{\sqrt{99}+\sqrt{98}}$)×($\sqrt{99}$+1)
分析 (1)根据分母有理化的方法,分别求出二次根式$\frac{1}{\sqrt{27}}$、$\sqrt{\frac{3}{8}}$、$\frac{3}{\sqrt{7}-2}$的有理化因式即可;
(2)分别把每个二次根式的分子、分母同时乘以它们的有理化因式,将它们化简即可;
(3)首先根据分母有理化的方法,将每个二次根式化简,然后再根据平方差公式,求出算式的值是多少即可.
解答 解:(1)二次根式$\frac{1}{\sqrt{27}}$、$\sqrt{\frac{3}{8}}$、$\frac{3}{\sqrt{7}-2}$的有理化因式分别为 $\sqrt{3}、\sqrt{2}、\sqrt{7}+2$;
(2)$\frac{1}{\sqrt{27}}$=$\frac{1}{3\sqrt{3}}$=$\frac{1×\sqrt{3}}{3\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{3}}{9}$;
$\sqrt{\frac{3}{8}}$=$\frac{\sqrt{3}}{\sqrt{8}}=\frac{\sqrt{3}×\sqrt{2}}{2\sqrt{2}×\sqrt{2}}=\frac{\sqrt{6}}{4}$;
$\frac{3}{\sqrt{7}-2}$=$\frac{3×(\sqrt{7}+2)}{(\sqrt{7}-2)(\sqrt{7}+2)}=\frac{3×(\sqrt{7}+2)}{3}$=$\sqrt{7}+2$.
(3)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{\sqrt{99}+\sqrt{98}}$)×($\sqrt{99}$+1)
=($\sqrt{2}-1+\sqrt{3}-\sqrt{2}+2-\sqrt{3}+\sqrt{5}-2+…+\sqrt{99}$-$\sqrt{98}$)×($\sqrt{99}$+1)
=($\sqrt{99}-1$)×($\sqrt{99}$+1)
=${(\sqrt{99})}^{2}{-1}^{2}$
=99-1
=98
故答案为:$\sqrt{3}、\sqrt{2}、\sqrt{7}+2$;$\frac{\sqrt{3}}{9}、\frac{\sqrt{6}}{4}、\sqrt{7}+2$.
点评 此题主要考查了分母有理化的含义,以及分母有理化的方法,要熟练掌握.

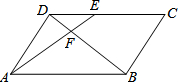 如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则S△ADF:S四边形BCEF为( )| A. | 10:31 | B. | 10:21 | C. | 4:25 | D. | 4:21 |
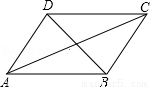
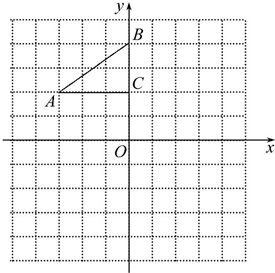 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).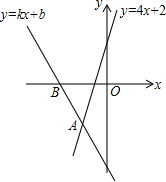 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b<4x+2<0 的解集为-1<x<-$\frac{1}{2}$.