题目内容
20.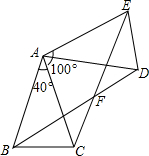 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.
如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD和CE,BD与CE交于点F.(1)∠AEC的度数;
(2)求证:四边形ABFE是菱形.
分析 (1)根据旋转可得∠CAE=100°,AC=AE,再根据三角形内角和定理可得∠AEC的度数;
(2)首先证明∠BAE=∠BFE,∠ABD=∠ADB=∠ACE=∠AEC,再根据对角相等的四边形是平行四边形,可证得四边形ABFE是平行四边形,然后再根据旋转可得AE=AB,依据邻边相等的平行四边形是菱形,即可证得.
解答 (1)解:根据旋转可得∠CAE=100°,AC=AE,
∵∠AEC+∠ACE+∠CAE=180°,
∴∠AEC=$\frac{1}{2}$(180°-100°)=40°;
(2)证明:证明:∵∠BAD=∠CAE=100°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=40°.
∵∠BAE=∠BAD+∠DAE=140°,
∴∠BFE=360°-∠BAE-∠ABD-∠AEC=140°,
∴∠BAE=∠BFE,
∴四边形ABFE是平行四边形,
∵AB=AE,
∴平行四边形ABFE是菱形.
点评 此题考查了等腰三角形的性质、旋转的性质以及菱形的判定,熟练掌握菱形的判定定理是解本题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
8.计算(-6)÷(-1)的结果等于( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | -7 |
15.在奥运会射击选手预选赛上,把甲、乙、丙三位选手各10次射击成绩的平均数和方差统计如表:
则射击成绩最稳定的选手是乙(选填“甲”“乙”“丙”中的一个)
| 选手 | 甲 | 乙 | 丙 |
| 平均数($\overline{x}$) | 9.3 | 9.3 | 9.3 |
| 方差(s2) | 0.026 | 0.015 | 0.032 |
8.一只蚂蚁沿数轴从点A向右直爬15个单位到达点B,点B表示的数为-2,则点A所表示的数为( )
| A. | 15 | B. | 13 | C. | -13 | D. | -17 |
 已知:如图,?ABCD中,∠BCD的平分线交AB于点E,交侧的延长线于点F.
已知:如图,?ABCD中,∠BCD的平分线交AB于点E,交侧的延长线于点F.